Абсолютными в статистике называются суммарные обобщающие показатели, характеризующие размеры, объемы, уровни, мощности, темпы и др. изменения величин.
Существуют: натуральные, стоимостные и условно-натуральные (условное топливо, эталонные лошадиные силы) измерители абсолютных величин.
Относительные статистические величины – это показатели в виде коэффициентов, характеризующих долю отдельных частей, изучаемой совокупности во всем ее объеме.
Относительные показатели при исследовании экономических явлений и процессов изучаются совместно с абсолютными показателями и обеспечивают сопоставимость сравниваемой и базовой величин.
Относительный показатель динамики (ОПД) представляет собой отношение уровня исследуемого процесса или явления за данный период времени (по состоянию на данный момент времени) к уровню этого же процесса или явления в прошлом:
ОПД 
или ОПД 
.
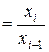Относительный показатель структуры (ОПС) представляет собой отношение структурных частей изучаемого объекта и их целого:
ОПС 
.
Выражается относительный показатель структуры в долях единицы или в процентах. Рассчитанные величины, соответственно называемые долями или удельными весами, показывают, какай долей обладает или какой удельный вес имеет та или иная часть в общем итоге.
Относительный показатель координации (ОПК) представляет собой отношение одной части совокупности к другой части этой же совокупности:
ОПК 
.
При этом в качестве базы сравнения выбирается та часть, которая имеет наибольший удельный вес или является приоритетной с экономической, социальной или какой-либо другой точки зрения. В результате получают величину, отражающую во сколько раз данная часть больше базисной или сколько процентов от нее составляет, или сколько единиц данной структурной части приходится на 1 единицу (иногда – на 100, 1000 и т.д. единиц) базисной структурной части.
Относительный показатель сравнения (ОПСр) представляет собой отношение одноименных абсолютных показателей, характеризующих разные объекты (предприятия, фирмы, районы, области, страны и т.п.):
ОПСр 
.
Относительные показатели плана и реализации плана используются для целей планирования и сравнения реально достигнутых результатов с ранее намеченными.
ОПП 
,
где, ОПП – относительный показатель плана;
– уровень, планируемый на i +1 период;
xi – уровень, достигнутый в i -м периоде.
Пример.
Оборот торговой фирмы в базисном году составил 2 млрд.руб. Руководство фирмы считает реальным в следующем году довести оборот до 2,8 млрд. руб. Найти ОПП, ОПРП, ОПД, если фактический оборот фирмы за отчетный год составил 2,6 млрд. руб.
ОПП = 
´ 100% = 140,0%;
ОПРП = 
´ 100% = 92,9%.
ОПД = 1,4·0,929 = 
=1,3 или 130%.
Средние величины
Средняя величина является обобщающей характеристикой совокупности однотипных явлений по изучаемому признаку. Средняя величина должна вычисляться с учетом экономического содержания определяемого показателя.
Таблица 4. Виды средних величин
| k | Наименование средней | Формула средней | Когда используется |
| Средняя арифметическая простая (невзвешенная) |  (1.2)
где xi – i-й вариант осредняемого признака ( ); n – число вариант
| Используется, когда расчет осуществляется по несгруппированным данным | |
| Средняя арифметическая взвешенная |  (1.3),
где fi – частота повторяемости i-го варианта
| Используется, когда данные представлены в виде рядов распределения или группировок | |
| -1 | Средняя гармоническая взвешенная |  (1.4), где  .
| Используется, когда известны индивидуальные значения признака и веса W за ряд временных интервалов |
| -1 | Средняя гармоническая невзвешенная |  (1.5)
| Используется в случае, когда веса равны |
| Средняя геометрическая невзвешенная |  (1.6)
| Используется в анализе динамики для определения среднего темпа роста | |
| Средняя геометрическая взвешенная |  (1.7)
| ||
| Средняя квадратическая невзвешенная |  (1.8)
| Используется при расчете показателей вариации | |
| Средняя квадратическая взвешенная |  (1.9)
|
