Невозможен процесс, единственным результатом которого была бы передача энергии путем теплообмена от тела с низкой температурой к телу с более высокой температурой

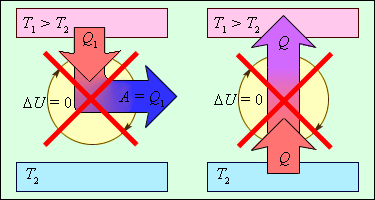
На рис. 3.12.2 изображены процессы, запрещаемые вторым законом, но не запрещаемые первым законом термодинамики. Эти процессы соответствуют двум формулировкам второго закона термодинамики.

Рисунок 3.12.2. Процессы, не противоречащие первому закону термодинамики, но запрещаемые вторым законом: 1 – «вечный двигатель второго рода»; 2 – самопроизвольный переход тепла от холодного тела к более теплому («идеальная холодильная машина»).

Следует отметить, что обе формулировки второго закона термодинамики эквивалентны. Если допустить, например, что тепло может самопроизвольно (то есть без затраты внешней работы) переходить при теплообмене от холодного тела к горячему, то можно прийти к выводу о возможности создания «вечного двигателя второго рода». Действительно, пусть реальная тепловая машина получает от нагревателя количество теплоты Q₁ и отдает холодильнику количество теплоты Q₂. При этом совершается работа A = Q₁ – |Q₂|. Если бы количество теплоты |Q₂| самопроизвольно переходило от холодильника к нагревателю, то конечным результатом работы реальной тепловой машины и «идеальной холодильной машины» было бы превращение в работу количества теплоты Q₁ – |Q₂|, полученного от нагревателя без какого-либо изменения в холодильнике. Таким образом, комбинация реальной тепловой машины и «идеальной холодильной машины» равноценна «вечному двигателю второго рода». Точно также можно показать, что комбинация «реальной холодильной машины» и «вечного двигателя второго рода» равноценна «идеальной холодильной машине».

Второй закон термодинамики связан непосредственно с необратимостью реальных тепловых процессов. Энергия теплового движения молекул качественно отличается от всех других видов энергии – механической, электрической, химической и т. д. Энергия любого вида, кроме энергии теплового движения молекул, может полностью превратиться в любой другой вид энергии, в том числе и в энергию теплового движения. Последняя может испытать превращение в любой другой вид энергии лишь частично. Поэтому любой физический процесс, в котором происходит превращение какого-либо вида энергии в энергию теплового движения молекул, является необратимым процессом, то есть он не может быть осуществлен полностью в обратном направлении.

Общим свойством всех необратимых процессов является то, что они протекают в термодинамически неравновесной системе и в результате этих процессов замкнутая система приближается к состоянию термодинамического равновесия.

На основании любой из формулировок второго закона термодинамики могут быть доказаны следующие утверждения, которые называются теоремами Карно:

1. Коэффициент полезного действия тепловой машины, работающей при данных значениях температур нагревателя и холодильника, не может быть больше, чем коэффициент полезного действия машины, работающей по обратимому циклу Карно при тех же значениях температур нагревателя и холодильника.
2. Коэффициент полезного действия тепловой машины, работающей по циклу Карно, не зависит от рода рабочего тела, а только от температур нагревателя и холодильника.

Таким образом, коэффициент полезного действия машины, работающей по циклу Карно, максимален.

Знак равенства в этом соотношении соответствует обратимым циклам. Для машин, работающих по циклу Карно, это соотношение может быть переписано в виде

В каком бы направлении ни обходился цикл Карно (по или против часовой стрелки), величины Q₁ и Q₂ всегда имеют разные знаки. Поэтому можно записать

Это соотношение может быть обобщено на любой замкнутый обратимый процесс, который можно представить как последовательность малых изотермических и адиабатических участков (рис. 3.12.3).

Рисунок 3.12.3. Произвольный обратимый цикл как последовательность малых изотермических и адиабатических участков.

При полном обходе замкнутого обратимого цикла

где ΔQ_i = ΔQ_1i + ΔQ_2i – количество теплоты, полученное рабочим телом на двух изотермических участках при температуре T_i. Для того, чтобы такой сложный цикл провести обратимым путем, необходимо рабочее тело приводить в тепловой контакт со многими тепловыми резервуарами с температурами T_i. Отношение ΔQ_i / T_i называется приведенным теплом. Полученная формула показывает, что полное приведенное тепло на любом обратимом цикле равно нулю. Эта формула позволяет ввести новую физическую величину, которая называется энтропией и обозначается буквой S (Р. Клаузиус, 1865 г.). Если термодинамическая система переходит из одного равновесного состояния в другое, то ее энтропия изменяется. Разность значений энтропии в двух состояниях равна приведенному теплу, полученному системой при обратимом переходе из одного состояния в другое.

В случае обратимого адиабатического процесса ΔQ_i = 0 и, следовательно, энтропия S остается неизменной.

Выражение для изменения энтропии ΔS при переходе неизолированной системы из одного равновесного состояния (1) в другое равновесное состояние (2) может быть записано в виде

Энтропия определена с точностью до постоянного слагаемого, так же, как, например, потенциальная энергия тела в силовом поле. Физический смысл имеет разность ΔS энтропии в двух состояниях системы. Чтобы определить изменение энтропии в случае необратимого перехода системы из одного состояния в другое, нужно придумать какой-нибудь обратимый процесс, связывающий начальное и конечное состояния, и найти приведенное тепло, полученное системой при таком переходе.

Рис. 3.12.4 иллюстрирует необратимый процесс расширения газа «в пустоту» в отсутствие теплообмена. Только начальное и конечное состояния газа в этом процессе являются равновесными, и их можно изобразить на диаграмме (p, V). Точки (a) и (b), соответствующие этим состояниям, лежат на одной изотерме. Для вычисления изменения ΔS энтропии можно рассмотреть обратимый изотермический переход из (a) в (b). Поскольку при изотермическом расширении газ получает некоторое количество теплоты от окружающих тел Q > 0, можно сделать вывод, что при необратимом расширении газа энтропия возросла: ΔS > 0.

Рисунок 3.12.4. Расширение газа в «пустоту». Изменение энтропии где A = Q – работа газа при обратимом изотермическом расширении.

Другой пример необратимого процесса – теплообмен при конечной разности температур. На рис. 3.12.5 изображены два тела, заключенные в адиабатическую оболочку. Начальные температуры тел T₁ и T₂ < T₁. При теплообмене температуры тел постепенно выравниваются. Более теплое тело отдает некоторое количество теплоты, а более холодное – получает. Приведенное тепло, получаемое холодным телом, превосходит по модулю приведенное тепло, отдаваемое горячим телом. Отсюда следует, что изменение энтропии замкнутой системы в необратимом процессе теплообмена ΔS > 0.

Рисунок 3.12.5. Теплообмен при конечной разности температур: a – начальное состояние; b – конечное состояние системы. Изменение энтропии ΔS > 0.

Рост энтропии является общим свойством всех самопроизвольно протекающих необратимых процессов в изолированных термодинамических системах. При обратимых процессах в изолированных системах энтропия не изменяется:

Это соотношение принято называть законом возрастания энтропии.