В шестой главе излагаются вопросы практического приложения теории процентных ставок в финансовых расчетах. Основная цель данной главы – показать и обосновать возможности использования финансовой математики в прикладных финансовых задачах. В главе изложены следующие вопросы:
1. Изменение условий контрактов. Консолидирование задолженности на основе процентных ставок разного вида.
2. Определение доходности ссудных и учетных операций с учетом удержания комиссионных.
3. Доходность операций с ценными бумагами.
4. Доходность купли и продажи финансовых инструментов.
Изменение условий контрактов
Финансовая эквивалентность обязательств предполагает неизменность (эквивалентность) финансовых отношений сторон до и после изменения условий. Эквивалентными считаются такие платежи, которые будучи «приведенными» по заданной процентной ставке к одному моменту времени оказываются равными. Приведение разновременно выплачиваемых платежей осуществляется путем дисконтирования (приведения к более ранней дате) или, наоборот, наращения, если эта дата относится к будущему периоду.
Принцип эквивалентности обязательств лежит в основе многих финансовых расчетов долгосрочного и краткосрочного характера. Он применяется при различного рода изменениях условий контрактов: их объединении, замене, долгосрочном погашении или пролонгировании.
Консолидирование задолженности на основе простой процентной ставки
Рассмотрим случай консолидирования платежей. Пусть платежи S1, S2, …Sm имеют сроки n1, n2, …. nm. Они объединяются в один платеж S0 со сроком n0. Необходимо найти размер нового платежа S0.
Если новый срок n0 больше сроков старых платежей, то размер нового платежа равен сумме консолидируемых платежей, наращенных по принятой ставке на момент выплаты S0.
S0=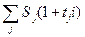 
,
где tj = n0 – nj.
Пример 26.
Два платежа 100 тыс.руб. и 50 тыс.руб. со сроками 150 и 180 дней (отсчитываемых от одной даты) заменяются одним со сроком 200 дней. Используется ставка простых процентов 6% годовых. Найти размер нового платежа.
Решение.
Для первого платежа срок пролонгации составляет 50 дней, для второго 20 дней. Консолидированный платеж находится суммированием наращенных платежей за соответствующие сроки.
S0 = 100000 (1 + 0,06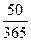 
) + 50000 (1 + 0,06 
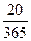) = 150986 (руб.)
В общем случае искомую величину S0 находят как сумму наращенных или дисконтированных платежей Sj:
S0 = +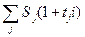 
,
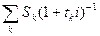где Sj – платежи со сроками
nj: nj < no, tj = n0 - nj
Sk -платежи со сроками n k: nk >n0 , tk = nk –n0.
Пример 27.
Решено консолидировать три платежа 10 тыс.руб., 20 тыс.руб., 15 тыс.руб. со сроками 15.05, 15.06, 15.08. Срок консолидированного платежа 01.08. Найти размер нового платежа при использовании процентной ставки 8% годовых.
Решение.
Первый и второй платежи продляются на 78 и 47 дней соответственно. Следовательно, суммы 10000 руб. и 20000 руб. необходимо нарастить по ставке 8%. Срок третьего платежа сокращается на 14 дней, следовательно, 15000 руб. необходимо дисконтировать.
S0=10000 (1+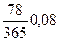 
) + 20000 (1+ 
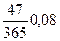) + 15000 (1+ 
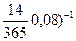=45331 (руб.)
