Физическое моделирование
Физическое моделирование, как правило применяют при постановке лабораторных экспериментов, что позволяет существенно уменьшить затраты на их проведение. Этим методом можно найти также решение задач, когда исследуемое явление настолько сложно, что не удается составить для него удовлетворительную математическую модель, либо решение сформулированной задачи встречает непреодолимые математические трудности.
При физическом моделировании сохраняется природа явлений и изменяется только его масштаб. Исследование модели, однако, позволяет получить достоверную информацию, если они построены по законам подобия. Подобными называют системы, геометрически подобные одна другой, у которых одноименные величины, характеризующие явление, относятся как постоянные числа, установленные на основе законов моделирования.
Коэффициент (масштаб) подобия сохраняет постоянное значение для всех точек данной системы. Коэффициент подобия изменяется, если одни подобные системы заменяются другими системами того же характера.
Теоремы подобия физических явлений составляют основу теории подобия и моделирования. Известны три теоремы подобия и ряд дополнительных положений подобия.
Первая теорема подобия рассматривает условия, следующие из подобия явлений. Если известно, что две рассматриваемые системы подобны, то у подобных явлений индикаторы подобия равны единице и критерии подобия численно одинаковы.
Критериями подобия называются составленные по определенным правилам и являющиеся одинаковыми для группы подобных процессов безразмерные комбинации физических величин. Критерии подобия обозначаются буквой  .
.
Вторая теорема подобия ( теорема) дает возможность замены уравнений физических величин более простыми зависимостями между критериями подобия. Она устанавливает, что если имеется уравнение
теорема) дает возможность замены уравнений физических величин более простыми зависимостями между критериями подобия. Она устанавливает, что если имеется уравнение
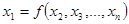
связывающее  переменных и физических параметров, то оно может быть заменено зависимостью
переменных и физических параметров, то оно может быть заменено зависимостью

где  – безразмерные величины, составленные по определенному закону из n величин (переменных и параметров), влияющих на ход процесса; m-число физических величин, имеющих независимые размерности (число основных единиц измерения должно быть больше или равно m).
– безразмерные величины, составленные по определенному закону из n величин (переменных и параметров), влияющих на ход процесса; m-число физических величин, имеющих независимые размерности (число основных единиц измерения должно быть больше или равно m).
В общем виде критерии подобия могут быть выражены
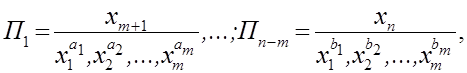
где  – некоторые постоянные числа, определяемые при решении уравнений, составленных с помощью приравнивания друг другу размерностей числителей и знаменателей каждого критерия.
– некоторые постоянные числа, определяемые при решении уравнений, составленных с помощью приравнивания друг другу размерностей числителей и знаменателей каждого критерия.
Теорема позволяет заменить переменные, сократив их число с  размерных величин до
размерных величин до  безразмерных величин. Это упрощает обработку аналитических и экспериментальных исследований, так как связь между
безразмерных величин. Это упрощает обработку аналитических и экспериментальных исследований, так как связь между  критериями оказывается проще, чем связь между n физическими величинами.
критериями оказывается проще, чем связь между n физическими величинами.
Уравнение, представляющее функцию критериев подобия, называется критериальным уравнением. Оно показывает, что один из  критериев подобия является функцией
критериев подобия является функцией  критериев.
критериев.
Третья, или обратная теорема подобия (теорема Кирпичева-Гухмана) устанавливает необходимые и достаточные условия для подобных явлений. Согласно этой теореме подобны между собой те явления, которые имеют подобные условия однозначности и одинаковые определяющие критерии подобия.
Смысл третьей теоремы заключается в том, что для подобия необходимо, чтобы они описывались одинаковыми математическими зависимостями. Определяющими критериями подобия называют критерии, состоящие из констант, характеризующих явление, и величин, являющихся независимыми аргументами, таких, например, как время, длина и другие, которые входят в условие однозначности.
Критерии подобия определяются двумя методами:
1) с помощью анализа размерностей при использовании  теоремы;
теоремы;
2) с помощью анализа систем уравнений.
Анализ размерностей, как метод получения критериев подобия, основан на анализе критериального уравнения, которое в соответствии со второй теоремой подобия записывается в виде
 /
/
Для механической системы общее количество физических величин, характеризующих процессы, 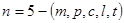 .
.
Здесь m – масса; p - сила; c - жесткость; l - геометрический параметр; t - время.






