При решении краевых задач математической физики выбор тех или иных координат диктуется, прежде всего, формой границы области, в которой сформулирована краевая задача. Так в предыдущем параграфе при решении задач для прямоугольных областей использовались прямоугольные декартовые координаты. Полярную систему координат целесообразно применять в тех случаях, когда граница тела совпадает с ее координатными линиями (круглые и кольцевые пластины, пластины в форме кругового или кольцевого сектора и т. п.). Во всех таких случаях использование полярных координат приводит к значительному упрощению решения задачи.
1.8.1. Основные уравнения плоской задачи в полярных координатах. В полярных координатах положение точки тела определяется координатами  и
и  , связанными с декартовыми координатами
, связанными с декартовыми координатами 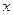 и
и 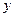 этой же точки уравнениями
этой же точки уравнениями

Вывод основных уравнений начнем со статических соотношений.
 Выделим из тела бесконечно малый объем, заключенный между координатными линиями
Выделим из тела бесконечно малый объем, заключенный между координатными линиями  ,
,  ,
,  ,
, 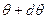 (см. рис. 1.10).
(см. рис. 1.10).
С точностью до линейных приращений на этот элемент действуют следующие напряжения: на грани  и
и  , — соответственно
, — соответственно 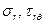 и
и 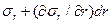 ,
,  , а на грани
, а на грани  и
и 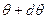 — соответственно
— соответственно 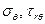 и
и  ,
,  . По аналогии с декартовыми координатами через
. По аналогии с декартовыми координатами через  и
и  мы обозначили нормальные напряжения на площадках, нормали к которым ориентированы вдоль координатных линий
мы обозначили нормальные напряжения на площадках, нормали к которым ориентированы вдоль координатных линий  и
и  а через
а через  , (
, ( ) — касательное напряжение.
) — касательное напряжение.
Принятое для них правило знаков показано на том же рисунке. Помимо напряжений на выделенный элемент действуют объемные силы, интенсивности проекций которых на координатные линии  и
и  мы обозначим через
мы обозначим через 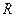 и
и 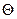 соответственно.
соответственно.
Составим уравнения равновесия элемента объема путем проектирования действующих на него сил на оси r и  , полагая, что толщина рассматриваемой пластины равна 1, а в силу малости угла
, полагая, что толщина рассматриваемой пластины равна 1, а в силу малости угла 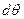

Тогда найдем
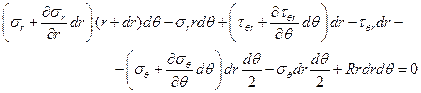
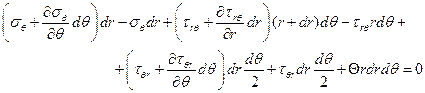
Приводя подобные члены и отбрасывая бесконечно малые величины третьего порядка малости, разделим оба уравнения на 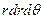 и перейдем к пределу, когда элемент объема подобным образом стягивается в точку
и перейдем к пределу, когда элемент объема подобным образом стягивается в точку  . Тогда приходим к следующим уравнениям локального равновесия в полярных координатах
. Тогда приходим к следующим уравнениям локального равновесия в полярных координатах

| (1.70) |
Мы приняли, что  . Доказать этот закон парности касательных напряжений можно путем рассмотрения равновесия элемента объема в отношении моментов вокруг оси
. Доказать этот закон парности касательных напряжений можно путем рассмотрения равновесия элемента объема в отношении моментов вокруг оси  . Но мы на этом не останавливаемся.
. Но мы на этом не останавливаемся.
В декартовых координатах уравнения равновесия при отсутствии объемных сил были удовлетворены введением функции напряжений. Аналогичный результат имеет место и в полярных координатах. Пусть  — функция напряжений. Тогда легко убедиться, что выражения
— функция напряжений. Тогда легко убедиться, что выражения

| (1.71) |
при 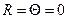 обращают уравнения (1.70) в тождества типа
обращают уравнения (1.70) в тождества типа 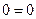 .
.
Обратимся теперь к геометрическим соотношениям. Условимся перемещения точки вдоль осей  и
и  обозначать символами
обозначать символами  и
и  , а деформации удлинения вдоль осей
, а деформации удлинения вдоль осей  ,
,  и деформацию сдвига (уменьшение прямого угла между осями
и деформацию сдвига (уменьшение прямого угла между осями  и
и  — символами
— символами 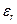 ,
, 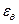 и
и 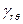 соответственно.
соответственно.
Выразим деформации через перемещения. С этой целью рассмотрим деформированное состояние  бесконечно малого элемента, показанное на рис.1.11. С точностью до линейных приращений можно записать
бесконечно малого элемента, показанное на рис.1.11. С точностью до линейных приращений можно записать

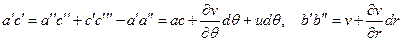

С учетом этих выражений по определению деформаций находим

| (1.72) |
Путем исключения из этих уравнений перемещений можно найти условие сплошности

| (1.73) |
 Закон Гука (1.61) сохраняет свой прежний вид и меняются лишь обозначения напряжении и деформаций.
Закон Гука (1.61) сохраняет свой прежний вид и меняются лишь обозначения напряжении и деформаций.
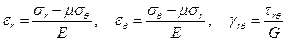
| (1.74) |
При решении плоской задачи в напряжениях помимо уравнений равновесия (1.70) следует привлечь условие сплошности (1.73), выраженное через напряжения. Подставляя (1.74) в (1.73) и преобразовывая их с помощью уравнений равновесия, получим

| (1.75) |
где
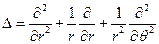
| (1.76) |
— дифференциальный оператор Лапласа в полярных координатах.
С учетом (1.71) уравнение Морриса Леви (1.75) примет вид

| (1.77) |
Это и есть разрешающее уравнение метода напряжений в полярных координатах. Это, по существу, — переписанное в полярных координатах уравнение (1.68).






