Для деяких частинних випадків функції 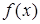 можна знайти частинні розв’язки диференціального рівняння (5.26) без квадратур.
можна знайти частинні розв’язки диференціального рівняння (5.26) без квадратур.
I). Розглянемо диференціальне рівняння з правою частиною
 , (5.37)
, (5.37)
де  поліном з дійсними чи комплексними коефіцієнтами,
поліном з дійсними чи комплексними коефіцієнтами,  -постійне дійсне чи комплексне число.
-постійне дійсне чи комплексне число.
Розглянемо два випадки.
Випадок 1. Число  не є коренем характеристичного рівняння. Тоді частинний розв’язок диференціального рівняння (5.37) шукають у вигляді
не є коренем характеристичного рівняння. Тоді частинний розв’язок диференціального рівняння (5.37) шукають у вигляді
 , (5.38)
, (5.38)
де
 (5.39)
(5.39)
поліном  -ої степені з невизначеними коефіцієнтами. Тобто, в цьому випадку частинний розв’язок має ту ж аналітичну структуру, що і права частина диференціального рівняння (5.37)
-ої степені з невизначеними коефіцієнтами. Тобто, в цьому випадку частинний розв’язок має ту ж аналітичну структуру, що і права частина диференціального рівняння (5.37)
Коефіцієнти 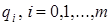 знаходяться шляхом підстановки (5.38) в (5.37) і прирівнювання коефіцієнтів при однакових степенях
знаходяться шляхом підстановки (5.38) в (5.37) і прирівнювання коефіцієнтів при однакових степенях 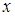 .
.
Переконаємося, що шукані коефіцієнти визначаються однозначно. Підставимо (5.38) в (5.37), отримаємо
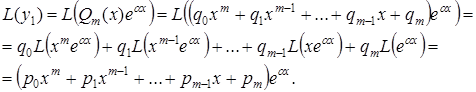
Використовуючи вищенаведені формули, запишемо
 .
.
На основі них маємо
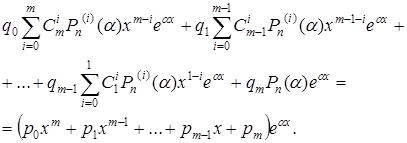
Скорочуємо на  і прирівнюємо коефіцієнти при однакових степенях
і прирівнюємо коефіцієнти при однакових степенях
 (5.40)
(5.40)
Так як 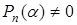 , то з (5.40) послідовно визначаються всі коефіцієнти
, то з (5.40) послідовно визначаються всі коефіцієнти 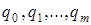 .
.
Випадок 2. Параметр  являється
являється  -кратним коренем характеристичного рівняння
-кратним коренем характеристичного рівняння 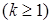 , тобто
, тобто
 . (5.41)
. (5.41)
В цьому випадку частинний розв’язок не можна побудувати в вигляді (5.38), так як  . Його шукаємо у вигляді
. Його шукаємо у вигляді
 , (5.42)
, (5.42)
де 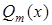 – поліном вигляду (5.39).
– поліном вигляду (5.39).
Коефіцієнти полінома визначаються шляхом підстановки (5.42) в (5.37).

Звідки
 .
.
Прирівнюємо коефіцієнти при однакових степенях
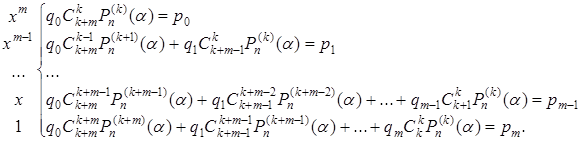 (5.43)
(5.43)
З (5.43) послідовно однозначно визначаються 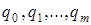 , так як
, так як  .
.
II). Припустимо, що права частина диференціального рівняння (5.26) має вигляд
 , (5.44)
, (5.44)
де 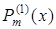 ,
,  – відомі поліноми степені менше або рівне
– відомі поліноми степені менше або рівне  (хоча б один має степінь
(хоча б один має степінь  ).
).
Використовуючи формули Ейлера, обчислимо
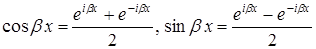
і перепишемо функцію 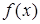 таким чином
таким чином

де 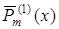 і
і 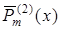 – поліноми степені
– поліноми степені  , тобто
, тобто 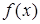 є сума двох функцій, які розглянуті вище.
є сума двох функцій, які розглянуті вище.
Випадок 1. Число  не є коренем характеристичного рівняння. Тоді частинний розв’язок шукаємо у вигляді
не є коренем характеристичного рівняння. Тоді частинний розв’язок шукаємо у вигляді
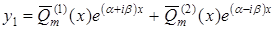 , (5.45)
, (5.45)
де 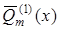 і
і 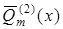 – поліноми
– поліноми  -ої степені з невизначеними коефіцієнтами.
-ої степені з невизначеними коефіцієнтами.
Випадок 2. Якщо  –
–  -кратний корінь характеристичного рівняння, то частинний розв’язок шукаємо в вигляді
-кратний корінь характеристичного рівняння, то частинний розв’язок шукаємо в вигляді
 . (5.46)
. (5.46)
Приводячи (5.45) і (5.46) до дійсного вигляду, сформулюємо наступне правило знаходження частинного розв’язку для випадку (5.44).
Випадок 1. Якщо  не є коренем характеристичного рівняння, то
не є коренем характеристичного рівняння, то
 . (5.47)
. (5.47)
Випадок 2. Якщо  –
–  -кратний корінь характеристичного рівняння (
-кратний корінь характеристичного рівняння (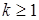 ), то
), то
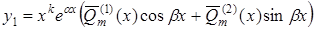 . (5.48)
. (5.48)
Тут 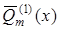 і
і 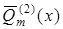 – поліноми
– поліноми  -ої степені з невизначеними коефіцієнтами.
-ої степені з невизначеними коефіцієнтами.
Приклад 5.12. Знайти загальний розв’язок диференціального рівняння методом невизначених коефіцієнтів
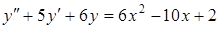 .
.
Розв'язання. Запишемо розв’язки однорідного диференціального рівняння
 ,
, 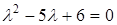 ,
,  ,
, 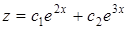 .
.
Знаходимо розв’язки неоднорідного диференціального рівняння
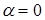 ,
,  ,
,  ,
,
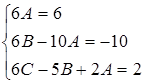 ,
,  .
.
Отже

– загальний розв’язок.
Приклад 5.13. Знайти загальний розв’язок диференціального рівняння методом невизначених коефіцієнтів
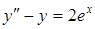 .
.
Розв'язання.  ,
,  ,
,  ,
, 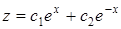 .
.
Так як  – корінь кратності
– корінь кратності 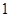 ,то
,то
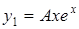 ,
,  ,
,

– загальний розв’язок.
Приклад 5.14. Знайти загальний розв’язок диференціального рівняння методом невизначених коефіцієнтів
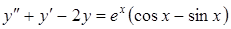 ..
..
Розв'язання. Для нашого випадку  .
.
Маємо 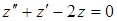 ,
,  ,
, 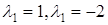 ,
,  .
.
Оскільки  , то
, то  . Після підстановки отримаємо
. Після підстановки отримаємо
 ,
,
 – загальний розв’язок.
– загальний розв’язок.
5.3. Неоднорідні лінійні диференціальні рівняння n -го порядку
5.3.1. Структура загального розв¢язку неоднорідного рівняння
Розглянемо неоднорідне диференціальне рівняння
 , (5.49)
, (5.49)
де 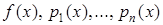 – неперервні на
– неперервні на 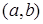 функції.
функції.
Припустимо, що для диференціального рівняння (5.49) ми знайшли частинний розв¢язок так, що
 . (5.50)
. (5.50)
Введемо нову змінну 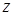
 . (5.51)
. (5.51)
Тоді
 .
.
Звідки
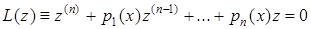 . (5.52)
. (5.52)
Диференціальне рівняння (5.52) називається однорідним диференціальним рівнянням, яке відповідає неоднорідному диференціальному рівнянню (5.49).
Загальний розв¢язок диференціального рівняння (5.52) записується у формі
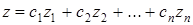 , (5.53)
, (5.53)
де 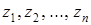 – фундаментальна система розв'язків диференціального рівняння (5.52),
– фундаментальна система розв'язків диференціального рівняння (5.52),  – довільні сталі. Тоді
– довільні сталі. Тоді
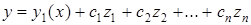 (5.54)
(5.54)
буде загальним розв¢язком диференціального рівняння (5.49) в області
 . (5.55)
. (5.55)
Таким чином, для знаходження загального розв¢язку неоднорідного диференціального рівняння (5.49) необхідно знайти один частинний розв¢язок диференціального рівняння (5.49) і прибавити до нього загальний розв¢язок однорідного диференціального рівняння.
Зауваження 5.1. Розглянемо диференціальне рівняння
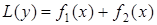 . (5.56)
. (5.56)
Припустимо, що 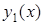 – частинний розв¢язок диференціального рівняння
– частинний розв¢язок диференціального рівняння 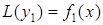 , а
, а 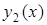 – частинний розв¢язок диференціального рівняння
– частинний розв¢язок диференціального рівняння 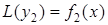 . Тоді, очевидно,
. Тоді, очевидно,  – частинний розв¢язок диференціального рівняння (5.56).
– частинний розв¢язок диференціального рівняння (5.56).
Приклад 5.15. Знайти частинний розв¢язок диференціального рівняння
 .
.
Розв'язання. Розглянемо диференціальні рівняння:
a) 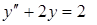 для якого
для якого  ;
;
b)  для якого
для якого 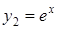 .
.
Тоді 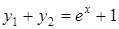 – частинний розв¢язок даного диференціального рівняння.
– частинний розв¢язок даного диференціального рівняння.
5.3.2. Метод варіації довільної сталої (метод Лагранжа)
Загальний розв¢язок неоднорідного диференціального рівняння(5.49) можна знайти в квадратурах, якщо відомо загальний розв¢язок відповідного однорідного диференціального рівняння (5.52). Будемо шукати загальний розв¢язок диференціального рівняння (5.49) у вигляді
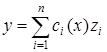 , (5.57)
, (5.57)
де  – деяка фундаментальна система розв¢язків диференціального рівняння (5.52).
– деяка фундаментальна система розв¢язків диференціального рівняння (5.52).
Виберемо функції  так, щоб функція (5.57) була загальним розв¢язком диференціального рівняння (5.49). Так як шукані функції задовольняють тільки одній умові, то для їх визначення можна підпорядкувати їх будь яким (n-1) умовам.
так, щоб функція (5.57) була загальним розв¢язком диференціального рівняння (5.49). Так як шукані функції задовольняють тільки одній умові, то для їх визначення можна підпорядкувати їх будь яким (n-1) умовам.
Таким чином, знайдемо n похідних функції (5.57):
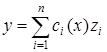 ;
;
 й покладемо
й покладемо  ;
;
 й покладемо;
й покладемо;  ;
;
………………..
 й покладемо
й покладемо  ;
;
 й покладемо
й покладемо  .
.
Підставляючи (5.58) в диференціальне рівняння (5.49) отримаємо n –е рівняння
 .
.
Таким чином, для визначення невідомих функцій отримаємо систему диференціальних рівнянь
 . (5.59)
. (5.59)
Відносно  – це система лінійних рівнянь з визначником
– це система лінійних рівнянь з визначником  . Для знаходження
. Для знаходження  запишемо формулу
запишемо формулу
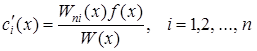 , (5.60)
, (5.60)
де  – алгебраїчне доповнення до елементу n- го рядка і i –го стовпчика визначника
– алгебраїчне доповнення до елементу n- го рядка і i –го стовпчика визначника 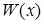 . Всі функції, які входять в праву частину диференціального рівняння (5.60) є неперервними на
. Всі функції, які входять в праву частину диференціального рівняння (5.60) є неперервними на 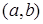 . З (5.60) отримаємо
. З (5.60) отримаємо
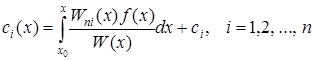 , (5.61)
, (5.61)
де  – довільні сталі,
– довільні сталі, 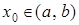 .
.
Тоді загальний розв¢язок диференціального рівняння (5.49) запишеться у вигляді
 . (5.62)
. (5.62)
Тут
 (5.63)
(5.63)
– частинний розв¢язок диференціального рівняння (5.49).
Неважко перевірити, що частинний розв¢язок (5.63) задовольняє нульовим початковим умовам
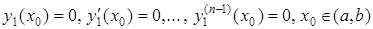 .
.
Приклад 5.16. Знайти загальний розв¢язок диференціального рівняння
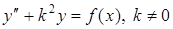 .
.
Розв'язання. Фундаментальна система розв¢язків для диференціального рівняння 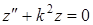 буде
буде  . Отже
. Отже
 .
.
Тому загальний розв¢язок запишемо у вигляді (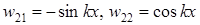 )
)
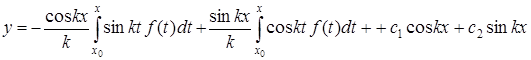 ,
,
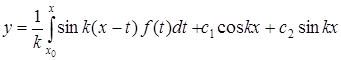 .
.
Зокрема, для диференціального рівняння другого порядку
 (5.64)
(5.64)
загальний розв¢язок запишеться у вигляді
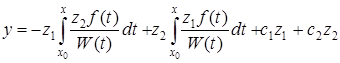 . (5.68)
. (5.68)
При цьому 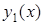 – частинний розв¢язок диференціального рівняння (5.64), який задовольняє цьому рівнянню з початковими умовами
– частинний розв¢язок диференціального рівняння (5.64), який задовольняє цьому рівнянню з початковими умовами 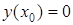 ,
,  .
.
Для диференціального рівняння виду
 , (5.66)
, (5.66)
так як 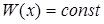 , що випливає з формули Остроградського – Ліувілля, загальний розв¢язок запишемо у формі
, що випливає з формули Остроградського – Ліувілля, загальний розв¢язок запишемо у формі
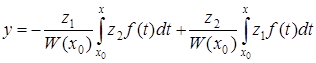 . (5.67)
. (5.67)
Таким чином, для знаходження загального розв¢язку диференціального рівняння (5.49) необхідно знайти фундаментальну систему розв¢язків однорідного рівняння (5.52), після чого загальний розв¢язок запишеться в квадратурах.
5.3.3. Знаходження частинного розв¢язку лінійного неоднорідного диференціального рівняння n –го порядку методом Коші
Припустимо, що для рівняння (5.52) відома фундаментальна система розв¢язків 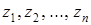 . Використовуючи (5.53), побудуємо частинний розв¢язок диференціального рівняння (5.52), який задовольняє початковим умовам
. Використовуючи (5.53), побудуємо частинний розв¢язок диференціального рівняння (5.52), який задовольняє початковим умовам
 . (5.68)
. (5.68)
Цей розв¢язок буде залежати від  , як від параметра
, як від параметра 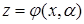 . Тут
. Тут  , функція
, функція 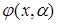 має неперервні частинні похідні по
має неперервні частинні похідні по 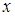 та
та  до n –го порядку включно. Причому, вона є розв¢язком диференціального рівняння (5.52)
до n –го порядку включно. Причому, вона є розв¢язком диференціального рівняння (5.52) 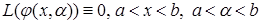 . Крім цього, в силу початкових умов (5.68), функція
. Крім цього, в силу початкових умов (5.68), функція 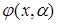 задовольняє умовам
задовольняє умовам
 , (5.69)
, (5.69)
де
 .
.
Умову (5.69) можна записати і так
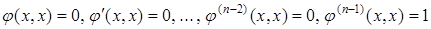 , (5.70)
, (5.70)
де
 .
.
Розглянемо функцію
 , (5.71)
, (5.71)
де  і покажемо, що ця функція є частинним розв¢язком диференціального рівняння (5.49) з початковими умовами
і покажемо, що ця функція є частинним розв¢язком диференціального рівняння (5.49) з початковими умовами
 .
.
Для цього використаємо формулу
 .
.
Знаходимо похідні
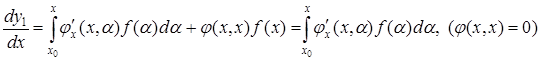 ,
,
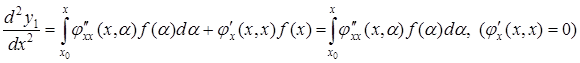 ,
,
………………………… (5.72)
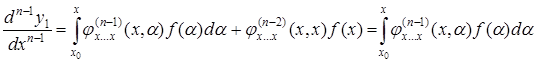
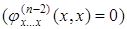 ,
,
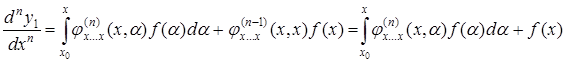
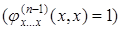 .
.
Підставимо (5.72) в диференціальне рівняння (5.49), отримаємо
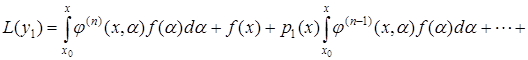

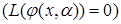 .
.
Тобто 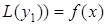 , а це означає, що функція (5.71) є частинним розв¢язком диференціального рівняння (5.49). Формула (5.71) називається формулою Коші.
, а це означає, що функція (5.71) є частинним розв¢язком диференціального рівняння (5.49). Формула (5.71) називається формулою Коші.
5.4. Лінійні диференціальні рівняння n –го порядку зі змінними коефіцієнтами, які зводяться до рівнянь з постійними коефіцієнтами
a). Рівняння Ейлера
Це рівняння вигляду
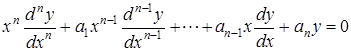 . (5.73)
. (5.73)
Це рівняння приводиться до рівняння з постійними коефіцієнтами заміною
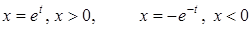 . (5.74)
. (5.74)
Дійсно
 ,
,
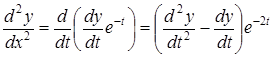 , (5.75)
, (5.75)
……………………
 .
.
Підставляючи (5.74) і (5.75) в диференціальне рівняння (5.73) ми отримаємо диференціальне рівняння n- го порядку з постійними коефіцієнтами
 . (5.76)
. (5.76)
Частинні розв¢язки диференціального рівняння (5.76) знаходять у вигляді 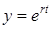 . Враховуючи (5.74), частинні розв¢язки диференціального рівняння (5.73) можна зразу шукати у вигляді (5.74)
. Враховуючи (5.74), частинні розв¢язки диференціального рівняння (5.73) можна зразу шукати у вигляді (5.74)
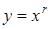 . (5.77)
. (5.77)
b). Рівняння Лагранжа має вигляд
 . (5.78)
. (5.78)
Це рівняння заміною  також приводиться до диференціального рівняння з постійними коефіцієнтами.
також приводиться до диференціального рівняння з постійними коефіцієнтами.
c). Рівняння
 (5.79)
(5.79)
називається рівнянням Чебишева і після заміни 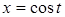 при
при  воно набирає вигляду
воно набирає вигляду
 . (5.80)
. (5.80)
Дійсно
 ,
,
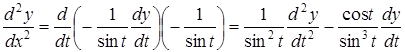 .
.
Отже
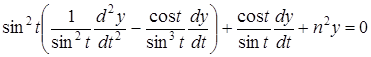 ,
,
 .
.
Тобто отримали (5.80).
Приклад 5.17. Розв¢язати диференціальне рівняння
 .
.
Розв'язання. Випишемо і розв¢яжемо характеристичне рівняння
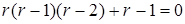 ,
,
 .
.
Тому фундаментальна система розв¢язків буде наступною
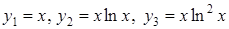 .
.
Отже
 – загальний розв¢язок.
– загальний розв¢язок.
5.5. Деякі питання теорії лінійних однорідних диференціальних рівнянь другого порядку. Задача Штурма – Ліувилля






