Для оптимальности допустимого вектора х= (х1,х2…,хn,) в задаче 1 достаточно существование m -мерного вектора у =(у1,…,уm), удовлетворяющего условиям:
а) уi і 0, i 
I2
б) еaijyi + cj = 0, j J1,
i I
в) еaijyi + cj, £ 0, j J2,
i I
г) еaijyi + cj, = 0, если хj >0 для j J2,
i I
д) уi = 0, если еaijxj + bi >0, i I2,
j J
тогда вектор у является оптимальным в задаче 1*.
Основная теорема теории линейного программирования
И ее следствия
Для разрешимости задачи математического программирования (как и в любой оптимизационной задачи) необходимо, чтобы множество допустимых решений было не пусто, и целевая функция на этом множестве была ограничена сверху (если задача на максимум), либо снизу (если задача на минимум).
Теорема двойственности. Каковы бы ни были исходные данные, для задач 1 и 1* имеет место один из следующих взаимоисключающих случаев.
1. В задачах 1 и 1* имеются оптимальные векторы х и у и 
, т.е. обе задачи разрешимы.
2. В задаче 1 существуют допустимые векторы, но линейная функция 
на множестве этих векторов не ограничена сверху, тогда в задаче 1* нет допустимых векторов.
3. В задаче 1* существуют допустимые векторы, но функция 
не ограничена снизу на множестве этих векторов, тогда в задаче 1 нет допустимых векторов.
4. В задачах 1 и 1* нет допустимых векторов.
Критерий разрешимости задачи ЛП
Теорема существования
Для того чтобы в двойственных задачах 1 и 1* существовали оптимальные векторы х и у, т.е. имел место случай 1 теоремы двойственности, достаточно выполнения одного из следующих условий:
1. в задаче 1 существует оптимальный вектор х
2. в задаче 1* существует оптимальный вектор у
3. в задаче 1 существует допустимый вектор х и функция 
ограничена сверху
4. в задаче 1* существует допустимый вектор у и функция 
ограничена снизу
5. в задачах 1 и 1* существуют допустимые векторы х и у
Необходимый признак оптимальности
Допустимый признак оптимальности в краткой и развернутой форме является также и необходимым признаком.
Доказательство: Пусть имеется оптимальный вектор х в задаче 1 и оптимальный вектор у в задаче 1*. Тогда на основании условий 2 теоремы о существовании имеет место случай 1 теоремы двойственности, то есть 
.
Прямые задачи линейного программирования в канонической форме
| Общая форма ЛП | 1 каноническая форма ЛП | 2 каноническая форма ЛП |
Задача 1. Максимизировать линейную функцию
на множестве векторов х= (х1,х2, …хn,),
удовлетворяющих условиям:
1. хj ³0 для jÎJ2
2. 
| Задача 2. Максимизировать функцию
на множестве векторов  удовлетворяющих условиям
1. 
2. 
I2=I ={1,2,…, m }
J2 J2 =J ={1,2,…, n }
| Задача 3. Максимизировать функцию
на множестве векторов  удовлетворяющих условиям:
1. 
2. 
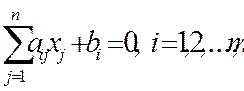I1=I ={1,2,…, m }
J2 J2 =J ={1,2,…, n }
|
