Некоторые определения
1. Пусть М = {a1, a2,..., а m } – множество вещественных чисел R.
Подмножество М называют ограниченным сверху, если все его элементы не превосходят некоторого с 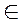 R, где величину «с» называют верхней границей для М.
R, где величину «с» называют верхней границей для М.
2. Для каждого ограниченного сверху непустого множества M  R имеется минимальная граница среди его верхних границ, которую называют супремумом множества М и обозначают sup M.
R имеется минимальная граница среди его верхних границ, которую называют супремумом множества М и обозначают sup M.
Если же множество M 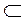 R не является ограниченным сверху, то пишут sup M=+
R не является ограниченным сверху, то пишут sup M=+  .
.
3. Множество М 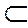 R называют ограниченным снизу, если все его элементы не меньше некоторого числа с
R называют ограниченным снизу, если все его элементы не меньше некоторого числа с 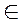 R.
R.
Для каждого ограниченного снизу непустого множества M 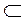 R имеется наибольшая граница среди его нижних границ, которую называют инфимумом множества М (inf M). Если же множество M
R имеется наибольшая граница среди его нижних границ, которую называют инфимумом множества М (inf M). Если же множество M 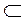 R не является ограниченным снизу, то пишут
R не является ограниченным снизу, то пишут
inf M =-  .
.
5. Система векторов x1, x2,…,xr, r ≥2, называется линейно зависимой, если хотя бы один из векторов системы является линейной комбинацией остальных, и линейно независимой – в противном случае.
Пример. Векторы  линейно зависимы.
линейно зависимы.
Линейная комбинация: 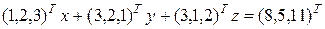 или
или
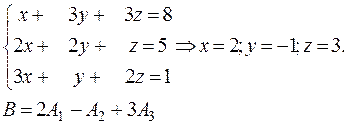
Векторы  - линейно независимы:
- линейно независимы:

6. Максимальное число линейно независимых векторов в n-мерном пространстве равно n.
7. Любая совокупность n линейно независимых векторов n-мерного пространства образует базис n-мерного пространства.
8. Какова бы ни была прямоугольная матрица А:
 ,
,
максимальное число линейно независимых строк (т. е. соответствующих n-мерных векторов) совпадает с максимальным числом линейно независимых столбцов (т. е. соответствующих m-мерных векторов). Это число называется рангом матрицы А.
Квадратную матрицу
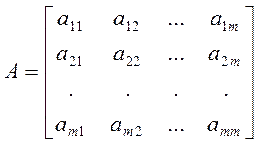
порядка m называют неособенной, если ее ранг r совпадает с m. Если отвечающая системе линейных уравнений  квадратная матрица А является неособенной, то эта система имеет единственное решение при любых свободных членах
квадратная матрица А является неособенной, то эта система имеет единственное решение при любых свободных членах  .
.
9. Любой вектор х, удовлетворяющий ограничениям задачи МП, называется допустимым вектором.
10. Допустимый вектор, доставляющий max или min целевой функции задачи ЛП, называется оптимальным вектором.
11. Если любые две точки множества D можно соединить ломаной, целиком лежащей в D, то множество D называется связным.
Некоторые важные теоремы
Кузнецов Ю.Н., Кузубов В.И. Волощенко А.В. Математическое программирование
Определение 1. Выпуклым называется множество, которое вместе с двумя точками содержит отрезок, их соединяющий.
Пусть  ,
, 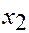 – две точки множества, возьмем произвольную точку
– две точки множества, возьмем произвольную точку  . Выразим
. Выразим  через
через  ,
, 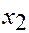 :
:
  
|
   выпуклая линейная комбинация, где выпуклая линейная комбинация, где  1, 1,  2 – угловые (крайние) точки.
Угловая точка не может быть представлена в виде выпуклой линейной комбинации.
Для угловых точек 2 – угловые (крайние) точки.
Угловая точка не может быть представлена в виде выпуклой линейной комбинации.
Для угловых точек 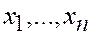 выпуклая линейная комбинация обобщается в виде: выпуклая линейная комбинация обобщается в виде:

 
|
Некоторые важные теоремы
Теорема 1. Множество всех допустимых решений задачи ЛП  выпукло.
выпукло.
€ Надо показать, что если  ,
, 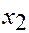 – допустимые решения задачи ЛП, то и
– допустимые решения задачи ЛП, то и  ,
, 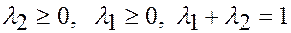 тоже допустимое решение.
тоже допустимое решение.
Имеем:  ■
■
Теорема 2. Целевая функция задачи ЛП достигает своего максимального значения в угловой точке допустимой области. Если целевая функция принимает максимальное значение в более чем одной угловой точке, то она достигает того же значения в любой точке, являющейся линейной комбинацией этих точек.
€ Пусть ОДР задачи ЛП ограничена и имеет угловые точки 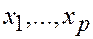 .
.
Пусть 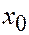 - оптимальное решение.
- оптимальное решение.
Имеем: (1) 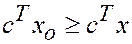 для любой точки из ОДР.
для любой точки из ОДР.
Пусть 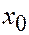 - не угловая точка (она м.б. представлена в виде выпуклой линейной комбинации).
- не угловая точка (она м.б. представлена в виде выпуклой линейной комбинации).
Тогда имеем: 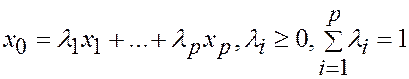
и 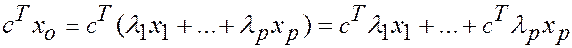
Среди  найдем максимальное:
найдем максимальное: 
Тогда: (2) 
Из (1), (2) имеем:  и
и 
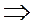

 - угловая точка.
- угловая точка.
Следовательно, существует угловая точка  , в которой целевая функция
, в которой целевая функция 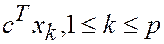 достигает максимального значения.
достигает максимального значения.
Если среди величин  имеются равные, т.е.
имеются равные, т.е.  , то для точек
, то для точек  образуем выпуклую линейную комбинацию
образуем выпуклую линейную комбинацию 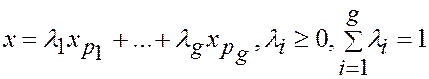 .
.
На основании предыдущей теоремы следует, что 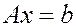 .
.
Определим 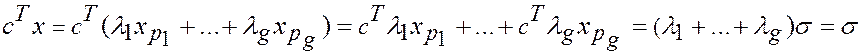 , т.е.
, т.е. 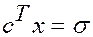 ■
■
Общая форма задачи ЛП
Пусть заданы: множества I ={1,2…m} и J= {1,2…n}, причем I= I1U I2, I1 Ç I2 = Æ, J= J1UJ2, J1Ç J2 = Æ, вещественные числа аij, bi, сj, iÎI, jÎJ.
ЗАДАЧА 1 (прямая со смешанными ограничениями)
Максимизировать линейную функцию
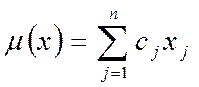 (1)
(1)
на множестве векторов х= (х1,х2, …хn,), (2)
удовлетворяющих условиям:
1. хj ³0 для jÎJ2 (3)
2.  (4)
(4)
Двойственная задача ЛП
ЗАДАЧА 1* (двойственная со смешанными ограничениями).
Минимизировать линейную функцию
 (5)
(5)
на множестве векторов y= (y1,y2,…..ym), (6)
удовлетворяющих условиям:
1. yi ≥ 0 для iÎI2 (7)
2.  (8)
(8)
Определение.
Векторы (2), (6), удовлетворяющие условиям (3), (4) и (7), (8) называются допустимым для задачи 1 и задачи 1* соответственно.
Допустимые векторы (2), (6), доставляющие максимум функции (1) и минимум функции (5) соответственно, называются оптимальными.
Связь между задачами 1 и 1*
Связь между парой двойственных задач устанавливает следующая лемма 1:
Для любых допустимых векторов х и у в задачах 1 и 1* выполняются неравенства
µ(x) £ 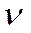 (у), (9)
(у), (9)
причем (9) выполняется как равенство в том и только в том случае, если справедливы следующие соотношения:
 (10)
(10)
 (11)
(11)
Связь между задачами 1 и 1*
 |
Доказательство. По условию  – допустимый вектор в задаче 1.
– допустимый вектор в задаче 1.


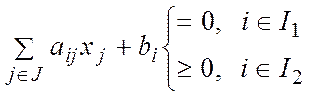
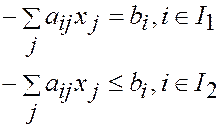
По условию  – допустимый вектор в задаче 1*.
– допустимый вектор в задаче 1*.



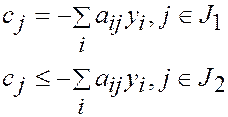


 µ (x) £ v (у)
µ (x) £ v (у)
Связь между задачами 1 и 1*(продолжение)
Доказательство.

 Полагаем:
Полагаем: 
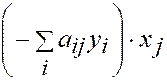 ,
, 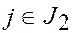

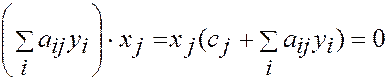

Аналогично,

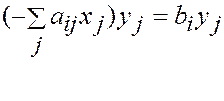
 ▄
▄
Признак оптимальности в краткой форме
Для оптимальности допустимого вектора х= (х1,х2, …хn,) в задаче 1 достаточно существования допустимого вектора y= (y1,y2,…..ym) в задаче 1*, удовлетворяющего условию
m (х) = n (у)(1)
Тогда допустимый вектор y= (y1,y2,…..ym) также является оптимальным в задаче 1*.
Доказательство.
Пусть вектор х допустимый и существует допустимый вектор у такой, что справедливо (1). Покажем, вектор х оптимальный.
Рассмотрим некоторый другой оптимальный вектор х′ в задаче 1 (х′≠х), тогда имеем пару векторов х′ и у. Для этой пары допустимых векторов справедлива лемма 1, т. е. m (х′) ≤ n (у) =m (х)и m (х′) ≤m (х). Отсюда следует что х – оптимальный вектор.
Покажем теперь, что вектор у также является оптимальным.
Рассмотрим некоторый другой оптимальный вектор у′ в задаче 1* (у′≠у), тогда имеем пару векторов х и у′. Для этой пары допустимых векторов справедливо лемма 1, т. е. n (у′)≥ m (х)= n (у) и n (у) ≤ n (у′). Отсюда следует что у – оптимальный вектор.▄






