Необходимое условие устойчивости

Свободные движения

Преобразуя дифференциальное уравнение (3.1) по Лапласу с учетом начальных условий: , получим

,

(3.2)

где — полином, коэффициенты которого зависят от начальных условий. Из алгебраического уравнения (3.2) легко получить изображение решения уравнения (3.1)

.

В том случае, когда характеристический полином системы имеет только простые корни: , выражение для свободных движений имеет вид

.

(3.3)

Здесь знак (¢) в выражении (3.3) означает дифференцирование полинома по s. Если корни полинома кратные, то вместо коэффициентов 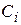в выражении (3.3) появятся полиномы от t со степенями ниже кратности корня .

Условие устойчивости

Как следует из выражения (3.3), необходимым и достаточным условием затухания экспонент является отрицательность действительных частей корней

.

(3.4)

На рис. 3.1 изображен пример расположения корней характеристического полинома асимптотически устойчивой системы пятого порядка на комплексной плоскости. Все корни находятся в открытой левой полуплоскости, т.е. строго левее мнимой оси. Поэтому часто говорят, что для асимптотической устойчивости системы необходимо и достаточно, чтобы все корни характеристического полинома были левыми. Это же условие справедливо и для собственных значений матрицы состояний A.

Рис. 3.1. Пример расположения корней устойчивой системы

Заметим, что если характеристический полином имеет простые корни на мнимой оси, то имеет место устойчивость по Ляпунову (но не асимптотическая).

Вынужденные движения неавтономных линейных систем представляются как сумма установившихся движений, определяемых полюсами изображений воздействий и переходных процессов из-за посленулевых начальных условий, вызванных внезапным приложением воздействий. Если системы асимптотически устойчивы, то с течением времени процессы стремятся к установившимся

.

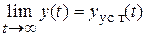Устойчивость вход-выход

Система называется устойчивой по входу, если при любом ограниченном воздействии f (t) ее реакция y (t) является ограниченной [58]. Устойчивость по входу характеризует свойство оператора преобразования вход-выход и анализируется по моделям (см. рис.1.18).

Устойчивость вход-выход в случае моделей рассматриваемого класса имеет место, если:

1 — система устойчива по начальным условиям, т.е. корни ее характеристического полинома находятся в левой полуплоскости;

2 — передаточная функция системы осуществима (физичечки реализуема), т. е. степень ее полинома числителя не превышает степень полинома знаменателя.

3.3. Критерии устойчивости

Для выявления устойчивости не обязательно знание корней, хотя в условиях применения ЭВМ их вычисление во многих случаях не представляет особых трудностей.

Для суждения об устойчивости системы или звена, не вычисляя корней характеристического полинома, применяют критерии устойчивости, которые с помощью относительно простых вычислений позволяют установить, лежат ли все корни в левой полуплоскости.

Различают алгебраические и частотные критерии устойчивости. К алгебраическим относятся критерии Гурвица (A. Hurwitz) и Рауса (E. Routh), а к частотным — критерии Михайлова и Найквиста (H. Nyquist).

Необходимое условие устойчивости

При определении устойчивости по характеристическому полиному, прежде всего, следует проверить выполнение необходимого условия: для того, чтобы все корни полинома имели отрицательные действительные части, все его коэффициенты должны быть одного знака (положительными).

Действительно, представим полином с единичным старшим коэффициентом как произведение двучленов , если , и трехчленов , если . В случае коэффициенты всех дву— и трехчленов положительны. Следовательно, положительны и все коэффициенты полинома . Для систем первого (n = 1) и второго (n = 2) порядка, это условие и достаточное; для 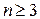необходимо выполнение дополнительных условий.

Типовое апериодическое звено первого порядка (n = 1) устойчиво при ; устойчивы и звенья второго порядка при . Интегрирующее (n = 1) и консервативное (n = 2) звенья не удовлетворяют условию положительности всех коэффициентов. Они имеют корни на мнимой оси. Это соответствует устойчивости по начальному состоянию (по Ляпунову); однако нет асимптотической устойчивости. Принято говорить, что звенья или системы, имеющие некратные корни характеристического полинома на мнимой оси (а остальные — левые) находятся на границе устойчивости. Такие системы являются негрубыми — они теряют устойчивость при сколь угодно малых изменениях параметров.

Алгебраические критерии

Пусть характеристический полином звена или системы автоматического управления имеет вид:

.

Критерий Гурвица. Для асимптотической устойчивости необходимо и достаточно, чтобы при все диагональные определители матрицы Гурвица были положительны.

Матрица Гурвица составляется из коэффициентов характеристического полинома следующим образом:

.

Это квадратная матрица . Ее диагональными определителями являются

Если выполнено необходимое условие положительности всех коэффициентов полинома, то вычисляются второй, последующие и предпоследний определители. Очевидно, последний определитель n -го порядка положителен при положительности определителя .

Например, для системы третьего порядка

(3.4)

матрица Гурвица имеет вид

 

.

Если выполнено необходимое условие положительности коэффициентов полинома , то следует проверять только знак определителя

. (3.5)

Для устойчивости системы третьего порядка произведение средних коэффициентов характеристического полинома должно быть больше произведения крайних.

С помощью критерия Гурвица можно строить границы устойчивости и выделять области устойчивости в пространстве коэффициентов полиномов или параметров системы автоматического управления.

Рассмотрим пример системы третьего порядка с характеристическим полиномом (3.4). Пусть все коэффициенты положительны. Проведем замену переменной, не приводящую к изменению расположения корней полинома относительно мнимой оси:

и получим другой полином

,

коэффициенты которого:

,

называют параметрами Вышнеградского. Границе устойчивости в плоскости параметров a, b соответствует гипербола Вышнеградского (рис. 3.2). Параметр нормировки W называется среднегеометрическим корнем, поскольку

 

Рис. 3.2. Диаграмма Вышнеградского (фрагмент)

Для систем высоких порядков критерий Гурвица не очень удобен — многократное вычисление определителей становится трудоемким и избыточным. Тогда предпочтительнее применение критерия Рауса, имеющего также алгоритмическую форму. Этот критерий позволяет быстро определить устойчивость системы, если имеется ее характеристический полином и заданы численно его коэффициенты.

Критерий Рауса наиболее экономичен по объему вычислений в сравнении с другими критериями. Он широко применяется для анализа влияния параметров системы на ее устойчивость с использованием вычислительных машин, поскольку алгоритм вычислений удобен для программирования.

Критерий Михайлова

Критерий Михайлова относят к частотным критериям. Он базируется на принципе аргумента [50]. Выражение для характеристического полинома рассматривается как функция комплексного переменного, принимающего значения на положительной мнимой полуоси. Критерий сводится к анализу изменения аргумента функции .

Согласно критерию Михайлова для устойчивости системы необходимо и достаточно, чтобы годограф вектора , начинаясь при w = 0 на действительной положительной полуоси, с ростом w от нуля до бесконечности обходил последовательно в положительном направлении (против часовой стрелки) n квадрантов, где n — порядок системы:

3.4. Устойчивость систем с типовой структурой

Рассмотрим системы, образованные последовательным и параллельным соединениями звеньев, а также системы с обратной связью.

Будем иметь в виду асимптотическую устойчивость по начальному состоянию, которая устанавливается по модели собственно системы .