Лекция № 3
Замена теоретической функции распределения F(х) на ее выборочный аналог Fn,(х) в определении математического ожидания, дисперсии, стандартного отклонения приводят к выборочному среднему, выборочной дисперсии, выборочному стандартному отклонению. Выборочные характеристики являются оценками соответствующих характеристик генеральной совокупности. Эти оценки должны удовлетворять определенным требованиям. В соответствии с важнейшими требованиями, оценки должны быть:
Ø несмещенными, то есть стремиться к истинному значению характеристики генеральной совокупности при неограниченном увеличении количества испытаний;
Ø состоятельными, то есть с ростом размера выборки оценка должна стремиться к значению соответствующего параметра генеральной совокупности с вероятностью, приближающейся к 1;
Ø эффективными, то есть для выборок равного объема используемая оценка должна иметь минимальную дисперсию.
Среди выборочных характеристик выделяют показатели, относящиеся к центру распределения (меры положения), показатели рассеяния вариант (меры рассеяния) и меры формы распределения. К показателям, характеризующим центр распределения, относят различные виды средних (арифметическое, геометрическое и т. п.), а также моду и медиану. Простейшим показателем, характеризующим центр выборки, является мода.
Мода — это элемент выборки с наиболее часто встречающимся значением (наиболее вероятная величина). При вычислении моды для интервального вариационного ряда необходимо сначала определить модальный интервал (по максимальной частоте), а затем — значение модальной величины признака по формуле:
где:
— значение моды
— нижняя граница модального интервала
— величина интервала
— частота модального интервала
— частота интервала, предшествующего модальному
— частота интервала, следующего за модальным
Средним значением выборки, или выборочным аналогом математического ожидания, называется величина
Иначе говоря, среднее значение — это центр выборки, вокруг которого группируются элементы выборки. При увеличении числа наблюдений среднее приближается к математическому ожиданию. Среднее значение обозначается также буквой М.
Выборочная медиана — это число, которое является серединой выборки, то есть половина чисел имеет значения большие, чем медиана, а половина чисел имеет значения меньше, чем медиана. Для нахождения медианы обычно выборку ранжируют — располагают элементы в порядке возрастания. Если количество членов ранжированного ряда нечетное, медианой является значение ряда, которое расположено посередине, то есть элемент с номером (п + 1)/2. Если число членов ряда четное, то медиана равна среднему членов ряда с номерами Ме = (n(число признаков в совокупности) + 1)/2. В случае четного числа признаков медиана будет равна средней из двух признаков находящихся в середине ряда.
При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана, а затем — значение медианы по формуле:
где:
— искомая медиана
— нижняя граница интервала, который содержит медиану
— величина интервала
— сумма частот или число членов ряда
- сумма накопленных частот интервалов, предшествующих медианному
— частота медианного интервала
Пример. Найти моду и медиану.
| Возрастные группы | Число студентов | Сумма накопленных частот ΣS |
| До 20 лет | ||
| 20 — 25 | ||
| 25 — 30 | ||
| 30 — 35 | ||
| 35 — 40 | ||
| 40 — 45 | ||
| 45 лет и более | ||
| Итого |
Решение:
В данном примере модальный интервал находится в пределах возрастной группы 25-30 лет, так как на этот интервал приходится наибольшая частота (1054).
Рассчитаем величину моды:
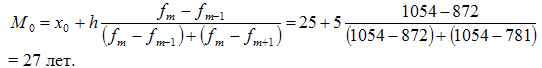
Это значит что модальный возраст студентов равен 27 годам.
Вычислим медиану. Медианный интервал находится в возрастной группе 25-30 лет, так как в пределах этого интервала расположена варианта, которая делит совокупность на две равные части (Σfi/2 = 3462/2 = 1731). Далее подставляем в формулу необходимые числовые данные и получаем значение медианы:
Это значит что одна половина студентов имеет возраст до 27,4 года, а другая свыше 27,4 года.
Кроме моды и медианы могут быть использованы такие показатели, как квартили, делящие ранжированный ряд на 4 равные части, децили -10 частей и перцентили — на 100 частей.
Лекция №4
Вариация — это различия индивидуальных значений признака у единиц изучаемой совокупности. Исследование вариации имеет большое практическое значение и является необходимым звеном в экономическом анализе. Необходимость изучения вариации связана с тем, что средняя, являясь равнодействующей, выполняет свою основную задачу с разной степенью точности: чем меньше различия индивидуальных значений признака, подлежащих осреднению, тем однороднее совокупность, а, следовательно, точнее и надежнее средняя, и наоборот. Следовательно по степени вариации можно судить о границах вариации признака, однородности совокупности по данному признаку, типичности средней, взаимосвязи факторов, определяющих вариацию.
Основными показатели рассеяния вариант являются интервал, дисперсия выборки, стандартное отклонение и стандартная ошибка.
Интервал (амплитуда, вариационный размах) это разница между максимальным и минимальным значениями элементов выборки. Интервал является простейшей и наименее надежной мерой вариации или рассеяния элементов в выборке.
Более точно отражают рассеяние показатели, учитывающие не только крайние, но и все значения элементов выборки.
Однако данный показатель имеет существенный недостаток. Его величина всецело зависит от крайних значений признака, он не учитывает всех изменений варьирующео признака в пределах совокупности. Поэтому в изучении вариации нельзя ограничиться определением лишь ее размаха.
Недостатком размаха вариации является и то, что он зависит от аномальных явлений. Поэтому следует очистить совокупность от аномальных наблюдений, прежде чем определить величину размаха вариации.
Другим показателем вариации служит среднее линейное отклонение (Ῑх). Оно вычисляется как средняя арифметическая из абсолютных значений отклонений хi от х (взвешенная или простая в зависимости от исходных условий) по следующим формулам:
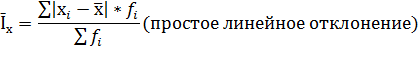
Поскольку сумма отклонений значений признака от средней величины равна нулю, необходимо все отклонения брать по модулю, на что указывают вертикальные линии в числителе формул.
Среднее линейное отклонение дает обобщенную характеристику степени колеблемости признаков совокупности. Однако чаще всего в статистической практике используют дисперсию (δ2) и среднеквадратическое отклонение (δ).
Данные показатели нашли также свое широкое применение в международной практике учета и статистического анализа, в частности в системе национального счетоводства.
Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины и вычисляется по формулам простой и взвешенной дисперсии (в зависимости от исходных данных):
Дисперсия есть средняя величина квадратов отклонений. Если извлечь из дисперсии корень второй степени, то получится среднее квадратическое отклонение (δ).
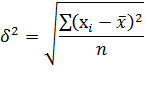
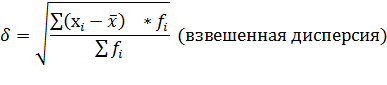
Среднее квадратическое отклонение – это обобщаюущая характеристика размеров вариации признака в совокупности. Оно выражается в тех же единицах измерения, что и признак (в метрах, тоннах, рублях, процентах и т.д.)
Выборочным стандартным отклонением (среднее квадратичное отклонение) называется величина
Это параметр, также характеризующий степень разброса элементов выборки относительно среднего значения. Чем больше среднее квадратичное отклонение, тем дальше отклоняются значения элементов выборки от среднего значения. Параметр аналогичен дисперсии и используется в тех случаях, когда необходимо, чтобы показатель разброса случайной величины выражался в тех же единицах, что и среднее значение этой случайной величины. Часто выборочное стандартное отклонение обозначают буквой σ (сигма).
Стандартная ошибка или ошибка среднего находится из выражения
Стандартная ошибка — это параметр, характеризующий степень возможного отклонения среднего значения, полученного на исследуемой ограниченной выборке, от истинного среднего значения, полученного на всей совокупности элементов. С помощью стандартной ошибки задается так называемый доверительный интервал. 95%-ный доверительный интервал, равный х+- 2m, обозначает диапазон, в который с вероятностью р = 0,95 (при достаточно большом числе наблюдений п> 30) попадает среднее генеральной совокупности МХ.
Выборочной квантилью называется решение уравнения
В частности, выборочная медиаана есть решение уравнения
Лекция 5
В симметричных распределениях средняя арифметическая, мода и медиана совпадают 
. Если это равенство нарушается — распределение ассиметрично.
Простейшим показателем ассиметрии является разность 
, которая в случае правосторонней ассиметрии положительна, а при левосторонней — отрицательна.
Для сравнения ассиметрии нескольких рядов вычисляется относительный показатель
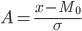
В качестве обобщающих характеристик вариации используются центральные моменты распределения 
-го порядка 
, соответствующие степени, в которую возводятся отклонения отдельных значений признака от средней арифметической:
Для несгруппированных данных:
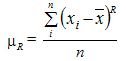
Для сгруппированных данных:
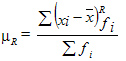
Момент первого порядка 
согласно свойству средней арифметической равен нулю 
.
Момент второго порядка 
является дисперсией 
.
Моменты третьего 
и четвертого 
порядков используются для построения показателей, оценивающих особенности формы эмпирических распределений.
С помощью момента третьего порядка измеряют степень скошенности или ассиметричности распределения.
— коэффициент ассиметрии
В симметричных распределениях 
, как все центральные моменты нечетного порядка. Неравенство нулю центрального момента третьего порядка указывает на асимметричность распределения. При этом, если 
, то асимметрия правосторонняя и относительно максимальной ординаты вытянута правая ветвь; если 
, то асимметрия левосторонняя (на графике это соответствует вытянутости левой ветви).
Для характеристики островершинности или плосковершинности распределения вычисляют отношение момента четвертого порядка () к среднеквадратическому отклонению в четвертой степени (
). Для нормального распределения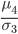 
, поэтому эксцесс находят по формуле:
Для нормального распределения 
обращается в нуль. Для островершинных распределений 
, для плосковершинных 
.
Эксцесс распределения
Кроме показателей, рассмотренных выше, обобщающей характеристикой вариации в однородной совокупности служит определенный порядок в изменении частот распределения в соответствии с изменениями величины изучаемого признака, называемый закономерностью распределения.
Характер (тип) закономерности распределения может быть выявлен путем построения вариационного ряда на основании большого объема наблюдений, а также такого выбора числа групп и величины интегралов, при котором наиболее отчетливо могла бы проявиться закономерность.
Анализ вариационных рядов предполагает выявление характера распределения (как результата действия механизма вариации), установление функции распределения, проверку соответствия эмпирического распределения теоретическому.
Эмпирическое распределение, полученное на основе данных наблюдения, графически изображается эмпирической кривой распределения с помощью полигона.
На практике встречаются различные типы распределений, среди которых можно выделить симметричные и асимметричные, одновершинные и многовершинные.
Установить тип распределения, означает выразить механизм формирования закономерности в аналитической форме. Многим явлениям и их признакам свойственны характерные формы распределения, которые аппроксимируются соответствующими кривыми. При всем многообразии форм распределения наибольшее распространение в качестве теоретических получили нормальное распределение, распределение Пауссона, биноминальное распределение и др.
Особое место в изучении вариации принадлежит нормальному закону, благодаря его математическим свойствам. Для нормального закона выполняется правило трех сигм, по которому вариация индивидуальных значений признака находится в пределах 
от величины средней. При этом в границах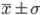 
находится около 70% всех единиц, а в пределах 
— 95%.
Оценка соответствия эмпирического и теоретического распределений производится с помощью критериев согласия, среди которых широко известны критерии Пирсона, Романовского, Ястремского, Колмогорова.
Часто значения асимметрии и эксцесса используют для проверки гипотезы о том, что данные (выборка) принадлежат к определенному теоретическому распределению, в частности, нормальному распределению. для нормального распределения асимметрия равна нулю, а эксцесс — трем.
В результате наблюдений или эксперимента получаются наборы данных, называемые выборками. для проведения их анализа данные подвергаются статистической обработке. Первое, что всегда делается при обработке данных, это вычисление элементарных статистических характеристик выборок (как минимум: среднего, среднеквадратичного отклонения, ошибки среднего) по каждому параметру и по каждой группе. Полезно также вычислить эти характеристики для объединения родственных групп и суммарно по всем данным.
Лабораторный практикум.
В мастере функций Ехсеl имеется ряд специальных функций, предназначенных для вычисления выборочных характеристик. Прежде всего, это функции, характеризующие центр распределения.
1. Функция СРЗНАЧ вычисляет среднее арифметическое из нескольких массивов (аргументов) чисел. Аргументы число 1, число2,... — это от 1 до 30 массивов, для которых вычисляется среднее.
Рис. «Основное окно функции СРЗНАЧ»
Например, если ячейки А1:А7содержат числа 10, 14,5,6, 10, 12 и 13, то средним арифметическим СРЗНАЧ(А1:А7) является 10.
2. Функция СРГАРМ позволяет получить среднее гармоническое множества данных. Среднее гармоническое — это величина, обратная к среднему арифметическому обратных величин. Например, с ГАРМ(10; 14;5;6; 10; 12; 13) равняется 8,317.
Рис. «Основное окно функции СРГАРМ»
3. Функция СРГЕОМ вычисляет среднее геометрическое значений массива положительных чисел. Функцию СРГЕОМ можно использовать для вычисления средних показателей динамического ряда. Например, СРГЕОМ (10; 14;5;6; 10; 12; 13) равняется 9,4 14.
Рис. «Основное окно функции СРГЕОМ».
4. Функция МЕДИАНА позволяет получать медиану заданной выборки. Медиана — это элемент выборки, число элементов выборки со значениями больше которого и меньше которого равно. Например, МЕДИАНА(10; 14;5;6; 10; 12; 13) равняется 10.
Рис. «Основное окно функции МЕДИАНА»
5. Функция МОДА вычисляет наиболее часто встречающееся значение в выборке. Например, МОДА (10;14;5;6;10;12;13) равняется 10.
Рис. «Основное окно функции МОДА»
К специальным функциям, вычисляющим выборочные характеристики, характеризующие рассеяние вариант, относятся ДИСП, СТАНДОТКЛОН, ПЕРСЕНТИЛЬ.
6. Функция ДИСП позволяет оценить дисперсию по выборочным данным. Например, ДИСП(10;14;5;6;10;12;13) равняется 11,667.
7. Функция СТАНДОТКЛОН вычисляет стандартное отклонение. Например, СТАНДОТКЛОН (10;14;5;6;10;12;13) равняется 3,416.
8. Функция ПЕРСЕНТИЛЬ позволяет получить квантили заданной выборки. Например, если ячейки А1:А7 содержат числа 10, 14, 5, 6, 10, 12 и 13, то квантилью со значением 0,1 является ПЕРСЕНТИЛЬ(А1:А7;0,1), равная 5,6.
Рис. «Основное окно функции ПЕРСЕНТИЛЬ»
Форму эмпирического распределения позволяют оценить специальные функции ЭКСЦЕСС и СКОС.
9. Функция ЭКСЦЕСС вычисляет оценку эксцесса по выборочным данным. Например, ЭКСЦЕСС (10;14;5;б;10;12;13) равняется —1,169.
10. Функция СКОС позволяет оценить асимметрию выборочного распределения. Например, ЭКСЦЕСС (10;14;5;6;10;12;13) равняется —0,527.
ПРИМЕР
Рассматриваются ежемесячные количества реализованных турфирмой путевок за периоды до и после начала активной рекламной компании. Ниже приведены количества реализованных путевок по месяцам. Требуется найти средние значения и стандартные отклонения этих данных.
| С рекламой | Без рекламы |
Решение
1. Для проведения статистического анализа прежде всего необходимо ввести данные в рабочую таблицу. Откройте новую рабочую таблицу. Введите в ячейку А1. слово Реклама, затем в ячейки А2:А8 — соответствующие значения числа реализованных путевок. В ячейку В1 введите слова Без рекламы, а в В2:В8 — значения числа реализованных путевок до начала рекламной компании. Отметим, что рассматриваемые группы данных со статистической точки зрения являются выборками.
Рис. «Основное окно с задачей»
2. При статистическом анализе прежде всего необходимо определить характеристики выборки, и важнейшей характеристикой является среднее значение. Для определения среднего значения в контрольной группе необходимо установить табличный курсор в свободную ячейку (А9). На панели инструментов нажмите кнопку Вставка функции (fx). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию СРЗНАЧ, после чего нажмите кнопку ОК. Появившееся диалоговое окно СРЗНАЧ за серое поле мышью отодвиньте вправо на 1—2 см от данных (при нажатой левой кнопке). Указателем мыши введите диапазон данных контрольной группы для определения среднего значения (А2:А8). Нажмите кнопку ОК. В ячейке А9 появится среднее значение выборки — 145,714.
Рис. «Окно функции СРЗНАЧ с выбранными параметрами»
В качестве упражнения определите в ячейке В9 среднее значение числа реализованных путевок без активной рекламы. Для этого табличный курсор установите в ячейку В9. На панели инструментов нажмите кнопку Вставка функции (fx) появившемся диалоговом окне выберите категорию Статистические и функцию СРЗНАЧ, после чего нажмите кнопку ОК. Появившееся диалоговое окно СРЗНАЧ за серое поле мышью отодвиньте вправо на 1—2 см от данных (при нажатой левой кнопке). Указателем мыши введите диапазон данных для определения среднего значения (В2:В8). Нажмите кнопку ОК. В ячейке В9 появится среднее значение выборки — 125,571.
З. Следующей по важности характеристикой выборки является мера разброса элементов выборки от среднего значения. Такой мерой является среднее квадратичное или стандартное отклонение. Для определения стандартного отклонения в контрольной группе необходимо установить табличный курсор в свободную ячейку (А10). На панели инструментов нажмите кнопку Вставка функции (fx). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию СТАНДОТКЛОН, после чего нажмите кнопку ОК. Появившееся диалоговое окно СТАНДОТКЛОН за серое поле мышью отодвиньте вправо на 1—2 см от данных (при нажатой левой кнопке). Указателем мыши введите диапазон данных контрольной группы для определения стандартного отклонения (А2:А8). Нажмите кнопку ОК. В ячейке А10 появится стандартное отклонение выборки 12,298. Существует правило, согласно которому при отсутствии артефактов данные должны лежать в диапазоне М ±3σ (в примере 145,736,9). В качестве упражнения требуется в ячейке В10 определить стандартное отклонение числа проданных путевок до начала рекламной компании. Для этого установите табличный курсор в ячейку В10. На панели инструментов нажмите кнопку Вставка функции. В появившемся диалоговом окне выберите категорию Статистические и функцию СТАНДОТКЛОН, после чего нажмите кнопку ОК. Появившееся диалоговое окно от данных (при нажатой левой кнопке). Указателем мыши введите диапазон данных для определения стандартного. отклонения (В2:В8). Нажмите кнопку ОК. В ячейке В10 появится стандартное отклонение выборки — 10,277.
Самостоятельное решение задач (домашнее задание)
1. Найдите среднее значение и стандартное отклонение результатов бега на дистанцию 100 м у группы студентов: 12,8; 13,2; 13,0; 12,9; 13,5; 13,1.
2. Найдите выборочные среднее, медиану, моду, дисперсию и стандартное отклонение для следующей выборки 26, 35, 29, 27, 33, 35, 30, 33, 31, 29.
3. Определите верхнюю (0,75) и нижнюю (0,25) квартили для выборки результатов измерений роста группы студенток: 164,160,157,166,162,160,161,159,160,163,170,171.
4. Определите выборочные асимметрию и эксцесс для данных измерений роста из упражнения.
Лекция 6. Использование инструментов Пакета анализа для вычисления выборочных характеристик.
В пакете Ехсеl помимо мастера функций имеется набор более мощных инструментов для работы с несколькими выборками и углубленного анализа данных, называемый Пакет анализа, который может быть использован для решения задач статистической обработки выборочных данных. Для установки раздела Анализ данных в пакете Ехсеl сделайте следующее:
Ø в меню Сервис выберите команду Надстройки;
Ø в появившемся списке установите флажок Пакет анализа.
Ввод данных. Исследуемые данные следует представить в виде таблицы, где столбцами являются соответствующие показатели. При создании таблицы Ехсеl информация вводится в отдельные ячейки. Совокупность ячеек, содержащих анализируемые данные, называется входным диапазоном.
Последовательность обработки данных. для использования статистического пакета анализа данных необходимо:
1. указать курсором мыши на пункт меню Сервис и щелкнуть левой кнопкой мыши;
2. в раскрывающемся списке выбрать команду Анализ данных (если команда Анализ данных отсутствует в меню Сервис, то необходимо установить в Ехсеl пакет анализа данных);
3. выбрать необходимую строку в появившемся списке Инструменты анализа;
4. ввести входной и выходной диапазоны и выбрать необходимые параметры.
Нахождение основных выборочных характеристик. Для определения характеристик выборки используется процедура Описательная статистика. Процедура позволяет получить статистический отчет, содержащий информацию о центральной тенденции и изменчивости входных данных, для выполнения процедуры необходимо:
5. выполнить команду Сервис Анализ данных;
6. в появившемся списке Инструменты анализа выбрать строку Описательная статистика и нажать кнопку ОК;
7. в появившемся диалоговом окне указать входной диапазон, то есть ввести ссылку на ячейки, содержащие анализируемые данные. Для этого следует навести указатель мыши на левую верхнюю ячейку данных, нажать левую кнопку МЫШИ и, не отпуская ее, протянуть указатель мыши к правой нижней ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши;
8. указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа. для этого следует поставить переключатель в положение Выходной диапазон (навести указатель мыши и щелкнуть левой клавишей), далее навести указатель мыши в поле ввода Выходной диапазон и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верхнюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши;
9. в разделе Группировка переключатель установить в положение по столбцам;
10. установить флажок в поле Итоговая статистика. Нажать кнопку ОК.
В результате анализа в указанном выходном диапазоне для каждого столбца данных выводятся следующие статистические характеристики: среднее, стандартная ошибка (среднего), медиана, мода, стандартное отклонение, дисперсия выборки, эксцесс, асимметричность, интервал, минимум, максимум, сумма, счет, наибольшее, наименьшее, уровень надежности.
Рис. «Окно описательной статистики».
Пример 4.
Рассматривается зарплата основных групп работников гостиницы: администрации, обслуживающего персонала иработников ресторана. Были получены следующие данные:
| Администрация | Персонал | Ресторан |
Необходимо определить основные статистические характеристики в группах данных.
Решение
1. Для использования инструментов анализа исследуемые данные следует представить в виде таблицы, где столбцами являются соответствующие показатели. Значения зарплат сотрудников администрации введите в диапазон А1:А5, обслуживающего персонала — в диапазон В1:В8 и т. д. В результате получится таблица, представленная на рис.:
Рис. 6.7. Таблица из примера 4
2. Далее необходимо провести элементарную статистическую обработку. Для этого, указав курсором мыши на пункт меню Сервис, выбрать команду Анализ данных. Затем в появившемся списке Инструменты анализа выбрать строку Описательная статистика.
Рис. Пример заполнения диалогового окна Описательная статистика
З. В появившемся диалоговом окне в рабочем поле Входной интервал укажите входной диапазон — А 1:С8. Активировав переключателем рабочее поле Выходной интервал, укажите выходной диапазон — ячейку А9. В разделе Группировка переключатель установите в положение по столбцам. Установите флажок в поле Итоговая статистика и нажмите кнопку ОК.
В результате анализа в указанном выходном диапазоне для каждого столбца данных получим соответствующие результаты
Рис. Результаты работы инструмента Описательная статистика
Все полученные характеристики были рассмотрены ранее в разделе «Выборочные характеристики», за исключением последних четырех:
Ø минимум — значение минимального элемента выборки;
Ø максимум — значение максимального элемента выборки;
Ø сумма — сумма значений всех элементов выборки;
Ø счет — количество элементов в выборке.
Среди этих характеристик наиболее важными являются показатели Среднее, Стандартная ошибка (среднего) и Стандартное отклонение.
Домашнее задание.
1. Найдите наиболее популярный туристический маршрут из четырех реализуемых фирмой (моду), если за неделю последовательно были реализованы следующие маршруты (приводятся номера маршрутов): 1, 3, 3, 2, 1, 1, 4, 4, 2, 4, 1, 3, 2, 4,1,4,4,3,1,2,3,4,1, 1,3.
2. 9. В рабочей зоне производились замеры концентрации вредного вещества. Получен ряд значений (в мг/м3): 12, 16, 15, 14, 10, 20, 16, 14, 18, 14, 15, 17, 23, 16. Необходимо определить основные выборочные характеристики.
