ЗАНЯТИЕ 5. Дифференциальные уравнения высших порядков.
План:
- Дифференциальное уравнение n-го порядка, зависящее только от переменной.
- Дифференциальное уравнение n-го порядка, не содержащее явно у и младших производных до порядка k-1 включительно.
- Дифференциальное уравнение n-го порядка, не содержащее явно независимой переменной.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Обыкновенным дифференциальным уравнением называется уравнение, связывающее между собой значения независимой переменной x, неизвестной функции y = f (x) и её производных (или дифференциалов): 
.
Опр. Порядком уравнения называется максимальный порядок n входящей в него производной (или дифференциала).
Опр. Частным решением уравнения на интервале (a, b) (конечном или бесконечном) называется любая n раз дифференцируемая функция 
, удовлетворяющая этому уравнению, т.е. обращающая уравнение на этом интервале в тождество.
Опр. Общим решением (общим интегралом) уравнения называется такое соотношение 
, что:
1. Любое решение 
этого соотношения относительно y (для набора постоянных C 1, C 2, …, Cn из некоторой области n -мерного пространства) является частным решением уравнения;
2. Любое частное решение уравнения может быть получено из общего решения при некотором наборе постоянных C 1, C 2, …, Cn.
Основную теорему - теорему о существовании и единственности решения задачи Коши для уравнения n -го порядка -мы сформулируем для записи уравнения в форме, разрешённой относительно старшей производной: 
.
Постановка задачи Коши для уравнения n -го порядка: требуется найти решение уравнения
| ;
|
удовлетворяющее начальным условиям
|
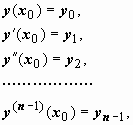
где y 0, y 1, y 2, …, yn -1 - заданные числа.
В случае уравнения второго порядка это означает, что требуется найти решение, проходящее через заданную точку (x 0, y 0,) с заданным угловым коэффициентом y 1.
НЕКОТОРЫЕ ТИПЫ УРАВНЕНИЙ, ДОПУСКАЮЩИЕ ПОНИЖЕНИЕ ПОРЯДКА.
1.Уравнение вида 
решается последовательным n -кратным интегрированием.
Пример1. 
Переобозначив постояные, общее решение запишем в виде
y = cos x + C 1 x 3 + C 2 x 2 + C 3 x + C 4.
2.Уравнение, не содержащее в явном виде неизвестную функцию и её младшие производные.
Порядок уравнения вида F (x, y (k), y (k +1), y (k +2), …, y (n)) = 0, не содержащего функции y (x) и k - 1 младшую производную этой функции в явном виде, может быть понижен ровно на k единиц введением новой неизвестной функции z (x) = y (k)(x).
Тогда 
z (n - k) = y (n)(x),
и относительно z (x) уравнение примет вид 
, т.е. будет уравнением n - k -го порядка.
После нахождения z (x) последовательным интегрированием решается уравнение
y (k) = z (x).
Пример2. Решить задачу Коши: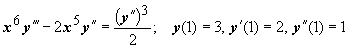 
. Младшая производная, входящая в явной форме в уравнения, - вторая, поэтому делаем замену искомой функции 
. Тогда 
, и уравнение примет вид 
. Это - уравнение Бернулли; пусть z = uv, тогда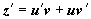 
, 
, 
, 
следовательно, 
. Относительно y (x) - это уравнение 
. Мы можем последовательно находить 
и так далее, однако в этом нет необходимости. Так как мы решаем задачу Коши, то из начального условия 
при x = 1 можно определить и знак частного решения, и значение постоянной C 1: 
. Теперь 
. Из условия 
при x = 1 находим C 2: 
; из условия y = 3 при x = 1 находим C 3: 
.
Окончательный ответ: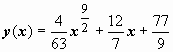 
.
3. Уравнение, не содержащее в явном виде независимую переменную x. Порядок уравнения 
, не содержащего явно x, может быть понижен на 1 с помощью красивого искусственного приёма, который заключается в том, что вводится новая функциональная зависимость 
от y: 
. Старшие производные y по x вычисляются по правилу дифференцирования сложной функции: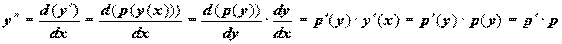 
.
Аналогично, 
Также находятся следующие производные, и всегда k -ая производная y по x выражается через k -1 -ую производную p по y.
В случае уравнения второго порядка 
в результате таких преобразований получим 
, т.е. уравнение первого порядка (в котором y выступает как аргумент, p (y) - как неизвестная функция). После нахождения решения p = p (y, C 1) этого уравнения решается уравнение 
, решение которого y = y (x, C 1, C 2) будет общим решением исходного уравнения.
Пример 3. Задача Коши 
.
Переменная x явно в уравнение не входит, поэтому полагаем , 
, тогда 
.
Просто сократить на p это уравнение нельзя, так как можно потерять семейство решений 
, поэтому рассматриваем два случая:
1. ;
2. 
Это - уравнение с разделяющимися переменными: 
.
Получено уравнение 
, решаем его: 
. Это общее решение уравнения, в данном случае оно включает в себя решение y = C при C 2 = 0.
Находим значения постоянных, при которых удовлетворяются начальные условия: из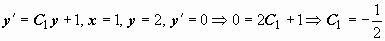 
.
Далее, из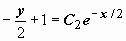 
следует, что 
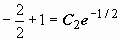, т.е. C 2 = 0.
Частное решение - 
, т.е. y = 2.
Пример 4.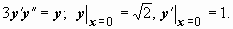 
Данное уравнение – уравнение 3 типа, поэтому вводим замену 
. Интеграл от дифференциала в левой части этого равенства вообще не берётся, поэтому проверим, не упростится ли задача, если использовать начальные условия. Так как при x = 0 должно быть 
, то получим 
.
Поэтому частное решение должно удовлетворять уравнению 
. Находим 
: 
.
Ответ: решение задачи Коши 
