Вопросы к экзамену по теории вероятностей
1. Комбинаторика: размещения, перестановки, сочетания, правило произведения. Примеры.
2.Определения: полной группы событий, несовместных, противоположных, равновозможных событий.
3.Определение вероятности (классическое, статистическое, геометрическое). Примеры.
4.Сумма событий. Вероятность суммы несовместных событий. Примеры.
5.Вероятность произведения. Зависимые и независимые события. Условная вероятность. Примеры.
6. Формула полной вероятности. Формула Байеса. Примеры.
7.Схема Бернулли. Примеры.
8. Дискретная случайная величина. Ряд распределения. Основное свойство ряда.
9.Математическое ожидание. Свойства.
10. Сумма случайных величин. Примеры. М.О. суммы случайных величин.
11. Дисперсия. Свойства.
12.Функция распределения случайной величины и ее свойства.
11.Плотность распределения случайной величины и ее свойства.
13. Биномиальное распределение. Нахождение числовых характеристик.
14. Равномерное распределение случайной величины. Примеры.
15. Нормальный закон распределения СВ. Исследование формы и построение кривой плотности распределения.
16. Нормальный закон распределения СВ. Смысл параметров.
17. Нормальный закон распределения СВ. Вероятность попадания в заданный интервал. 18. Правило трех сигм.
19. Свойства функции Лапласа.
20. Показательный закон распределения. Функция надежности.
Задача № 7, которую я выдала на занятии, неправильная. Надо решить другую, которая задана в варианте № 82
Индивидуальное домашнее задание по теории вероятностей.
ВГАВТ, факультет экономики и управления, 4-й семестр, 2012.
Билет № 82 (Для студента Заикина)
1. В коробке 20 конфет «Ассорти», из которых 10 штук с шоколадной начинкой, 6 штук с молочной начинкой и 4 штуки с джемом. Наугад взяты одновременно 3 конфеты. Найти вероятность того, что две из них с шоколадной начинкой и одна – с молочной.
2. Первое судно прибывает в порт по графику с вероятностью 
, второе с вероятностью - 
, третье с вероятностью 
. Найти вероятности следующих событий:
а) первое судно прибудет по графику, а второе и третье опоздают; б) два судна опоздают;
в) хотя бы одно судно опоздает.
3. Отчет в 80% случаев составляется первым сотрудником, в остальных случаях – вторым. Первый из сотрудников может допустить ошибку с вероятностью 0.01, второй с вероятностью – 0.2. Найти вероятность, что в отчете будет допущена ошибка.
4. В корзине находится 15 яблок одного сорта и 10 другого. Из корзины наугад вынимают три яблока. Составить закон распределения ДСВ 
- числа яблок первого сорта среди отобранных, найти математическое ожидание и дисперсию этой ДСВ.
5. Случайная величина задана интегральной функцией распределения
Найти плотность распределения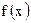 
, 
. Построить графики 
. Найти вероятность того, что СВ 
примет значение: а) меньшее, чем 7; б) не меньшее, чем 6,5; в) в промежутке (6,5;7,5).
6. Размер стержней, изготавливаемых станком, есть нормально распределенная СВ. Средний размер стержней 25 см., среднее квадратическое отклонение 0,4см. Найти: а) границы, в которых расположены размеры практически всех стержней; б) процент годных стержней, если допускается отклонение размера от среднего не более, чем на 0,6 см; в) вероятность того, что размер наугад взятого стержня будет заключен между 24,2 и 25,7 см; г) вероятность того, что из четырех наугад взятых стержней размер хотя бы двух из них будет заключен между 24,2 и 25,7 см.
7. Изучается процентное содержание меди в образцах. Случайно отобраны 500 образцов. Данные выборки:
| Содержание меди в образцах, % | 56-58 | 58-60 | 60-62 | 62-64 | 64-66 | 66-68 | 68-70 | 70-72 | 72-74 |
| Количество образцов |
На уровне значимости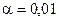 
проверить гипотезу о том, что С.В. - процентное содержание меди, подчиняется нормальному закону распределения. Для этого построить гистограмму, кривую теоретического распределения, вычислить статистику Пирсона 
, сравнить с критическим значением этой случайной величины.
Индивидуальное домашнее задание по теории вероятностей.
