Введение.
Очень часто физические процессы можно описать уравнениями или системой уравнений, которые содержат неизвестные функции и производные неизвестных функций или их дифференциалы. Такие уравнения или системы уравнений называются дифференциальными уравнениями или системой дифференциальных уравнений (дифуравнений). Основная задача состоит в нахождении неивестных функций, входящих в уравнение или систему уравнений. Если неизвестные функции зависят от одной независимой переменной, то дифуравнения называются обыкновенными. Если же неизвестные функции зависят от двух и более независимых переменных, то уравнение называется уравнением в частных производных.
Ограничимся рассмотрением обыкновенных дифуравнений и простейших систем обыкновенных дифуравнений.
При изучении неопределенного интеграла по производной или дифференциалу неизвестной функции находили саму функцию, т.е. решали дифуравнение  или
или 
Неизвестную функцию y(x) находим интегрированием, т.е. 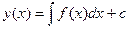 .
.
Обратим внимание на то, что полученное решение содержит бесконечно много функций, причем это решение зависит от одной произвольной постонной с.
Рассмотрим еще несколько задач, приводящих к понятию дифуравнения:
1. Задача о радиоактивном распаде.
Имеется  граммов радиоактивного вещества с периодам полураспада Т лет. Найти колличество нераспавшегося вещества за время t.
граммов радиоактивного вещества с периодам полураспада Т лет. Найти колличество нераспавшегося вещества за время t.
Решение. Через  обозначим колличество нераспавшегося вещества в момент времени t. Колличество распавшегося вещества за время
обозначим колличество нераспавшегося вещества в момент времени t. Колличество распавшегося вещества за время 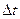 (т.е. за промежуток времени
(т.е. за промежуток времени  ) приближенно пропорционально колличеству наличного вещества
) приближенно пропорционально колличеству наличного вещества  и времени распада
и времени распада 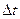 , т.е.
, т.е. 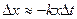 . Знак минус в правой части взят потому, что колличество вещества со временем убывает. Последнее равенство тем точнее, чем меньше
. Знак минус в правой части взят потому, что колличество вещества со временем убывает. Последнее равенство тем точнее, чем меньше 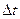 . Поделим обе части равенства на
. Поделим обе части равенства на 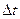 и перейдем к пределу при
и перейдем к пределу при 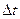 →0. В результате получим:
→0. В результате получим:  ,
,  ,
,  ,
,  ,
,  .
.
Получаем дифуравнение  относительно неизвестной функции
относительно неизвестной функции  .
.
Теперь остается решить полученное дифуравнение, т.е. найти неизвестную функцию  . Обе части уравнения
. Обе части уравнения  разделим на x и проинтегрируем:
разделим на x и проинтегрируем:  ;
;  ;
;  ;
;  .
.
Для нахождения  воспользуемся начальным условием:
воспользуемся начальным условием:  .
.
В решении  положим
положим 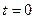 :
: 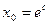 ;
;  .
.
Для нахождения коэффициента  воспользуемся тем, что период полураспада данного вещества равен
воспользуемся тем, что период полураспада данного вещества равен  лет.
лет.
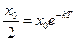 ;
;  ;
;  .
.
Обе части последнего равенства прологарифмируем по основанию 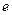 :
:
 ;
;  ;
;  ;
;  ;
;  - искомое решение.
- искомое решение.
2. Задача о механических колебаниях.
Задачи о колебаниях часто встречаются в физике, теоретической механике, при расчетах электрических цепей. С математической точки зрения многие задачи сводятся к решению следующей задачи: пусть материальная точка массы  (для простоты, положим
(для простоты, положим  ) движется прямолинейно. На точку действует восстанавливающая сила, стремящаяся вернуть точку в состояние равновесия, причем величина силы пропорциональна отклонению точки от положения равновесия. Далее, на точку действует сопротивление пропорциональное скорости движения. Кроме этого на точку действует посторонняя возмущающая сила
) движется прямолинейно. На точку действует восстанавливающая сила, стремящаяся вернуть точку в состояние равновесия, причем величина силы пропорциональна отклонению точки от положения равновесия. Далее, на точку действует сопротивление пропорциональное скорости движения. Кроме этого на точку действует посторонняя возмущающая сила  .
.
Для составления уравнения воспользуемся вторым законом Ньютона: произведение массы тела на ускорение равно сумме сил дайствующих на тело. Обозначается через  -расстояние точки от начального положения, получим:
-расстояние точки от начального положения, получим:  .
.  , где
, где
 - коэффициент сопротивления,
- коэффициент сопротивления,  коэффициент восстановления.
коэффициент восстановления.
Таким образом, получим дифуравнение, и поставленная задача сводится к решению дифуравнения, т.е. к нахождению неизвестной функции  .
.
Основные понятия.
Определение 1. Дифференциальным уравнением называется уравнение, содержащее независимую переменную, неизвестную функцию и производные неизвестной функции.
Дифференциальное уравнение в общем виде можно записать следующим образом:  , где
, где  -независимая переменная,
-независимая переменная,  -неизвестная функция.
-неизвестная функция.
Определение 2. Порядком дифференциальнрого уравнения называется наивысший порядок производной, входящей в уравнение.
Например:  является дифференциальным уравнением 2го порядка.
является дифференциальным уравнением 2го порядка.
Определение 3. Функция  называется решение дифуравнения, если при подстановке функции и ее соответствующих производных в уравнение, уравнение обращается в тождество.
называется решение дифуравнения, если при подстановке функции и ее соответствующих производных в уравнение, уравнение обращается в тождество.
Пример1. Показать, что функция  является решением уравнения
является решением уравнения  .
.
Решение. В самом деле, 
 Отсюда следует, что функция
Отсюда следует, что функция  является решением данного уравнения.
является решением данного уравнения.
Дифференциальные уравнения 1го порядка.
В общем виде дифференциальное уравнение первого порядка записывается следующим образом:  . (1)
. (1)
В частных случаях в левую часть уравнения в явном виде могут не входить  и
и  , но обязательно должна входить производная
, но обязательно должна входить производная  .
.
Если уравнение (1) можно разрешить относительно  , то его можно представить в следующем виде:
, то его можно представить в следующем виде:  (2)
(2)




