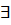 нейтральный элемент
нейтральный элемент 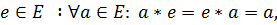
то есть элемент e не зависит от выбора a.
Примеры:
Для бинарной операции (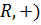 нейтральным элементом является нуль, т.е.
нейтральным элементом является нуль, т.е. 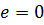 ;
;
Для бинарной операции (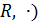 нейтральным элементом является единица, т.е.
нейтральным элементом является единица, т.е. 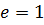 ;
;
Утверждение. Нейтральный элемент единственен.
Доказывается от противного.
⧠пусть существуют два нейтральных элемента 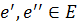 .
.
Умножим сначала элемент 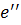 на первый нейтральный элемент
на первый нейтральный элемент 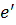 ,
,
потом наоборот элемент 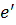 на второй нейтральный элемент
на второй нейтральный элемент 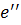 :
:
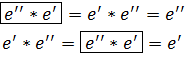
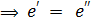

Наличие симметричного элемента
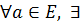 симметричныйему элемент
симметричныйему элемент 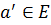 :
: 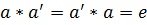 ,
,
то есть для каждого a существует свой симметричный.
Для сложения 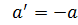 – противоположный элемент.
– противоположный элемент.
Для умножения 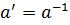 – обратный элемент.
– обратный элемент.
Note. Если бинарная операция односторонняя, то вводят понятие одностороннего нейтрального элемента и одностороннего симметричного элемента.
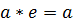
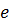
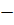 правосторонний нейтральный
правосторонний нейтральный
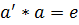
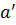
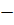 левосторонний симметричный
левосторонний симметричный
Для алгебраической операции  при выполнении условий 3) и 4) можно определить обратную операцию
при выполнении условий 3) и 4) можно определить обратную операцию 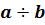 , положив
, положив 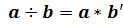
Для операции сложения условия 3) и 4) выполняются на множествах 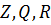 .
.
Поэтому, для операции сложения можно определить операцию вычитания,
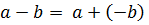 как сумму
как сумму 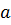 с числом противоположным
с числом противоположным 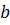 .
.
· На множестве N операцию вычитания определить нельзя
(нет нуля и нет противоположного элемента).
Для операции умножения условия 3) и 4) выполняются на множествах  отличных от нуля рациональных и действительных чисел.
отличных от нуля рациональных и действительных чисел.
Следовательно, на множествах 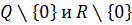 можно определить обратную к умножению операцию деления
можно определить обратную к умножению операцию деления 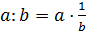 как произведение числа a на число, обратное к b.
как произведение числа a на число, обратное к b.
· На множестве целых чисел Z обратную умножению операцию деления определить нельзя (результат деления может не быть целым числом).
Таким образом, вычитание определено на множествах 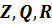 ,
,
а деление на множествах 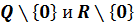 .
.
Дистрибутивность.
Рассмотрим множество (Е,  с двумя бинарными операциями
с двумя бинарными операциями 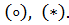
Операция  дистрибутивна относительно операции
дистрибутивна относительно операции 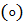
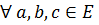
если она дистрибутивна
справа 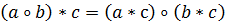 и слева
и слева 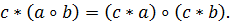
(R,+,  )двусторонняя дистрибутивность )двусторонняя дистрибутивность 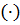 относительно (+) относительно (+)
| (R, 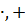 )(+) не дистрибутивная операцияотносительно )(+) не дистрибутивная операцияотносительно 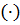
|
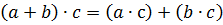

| 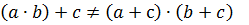
|
Дистрибутивность может быть односторонней.
(R,  ,^)
(^) дистрибутивная операция справа относительно ( ,^)
(^) дистрибутивная операция справа относительно (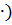
| (R,  ,^)
(^) не дистрибутивная операция слева относительно ( ,^)
(^) не дистрибутивная операция слева относительно (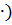
|
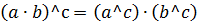 или или
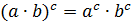
| 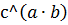 ≠ ≠ 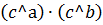 или или
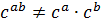
|
Группы, кольца, поля
· Множество (Е, 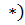 с одной бинарной операцией
с одной бинарной операцией 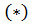 называется полугруппой (моноидом), если эта операция обладает свойством ассоциативности.
называется полугруппой (моноидом), если эта операция обладает свойством ассоциативности.
Пример полугруппы (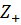 ,
,  +), (
+), (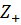 ,
,  )
)
· Множество G с одной бинарной операцией 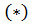 называется группой, если
называется группой, если
1) операцией 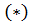 в G ассоциативна;
в G ассоциативна;
2) 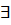 нейтральный элемент
нейтральный элемент 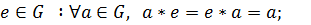
3) 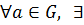 симметричный ему элемент
симметричный ему элемент 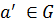 :
: 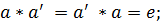
· Если операция  коммутативна, то группа называется коммутативной или абелевой, противном случае - некоммутативной.
коммутативна, то группа называется коммутативной или абелевой, противном случае - некоммутативной.
Относительно операции сложения группами являются множества Z, Q, R.
Относительно операции умножения группами являются множества 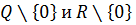 отличных от нуля рациональных и действительных чисел.
отличных от нуля рациональных и действительных чисел.
В группах по сложению нейтральный элемент 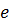 называется нулевым (или просто 0), а симметричный элемент
называется нулевым (или просто 0), а симметричный элемент 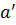 – противоположным
– противоположным 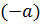 .
.
В группах по умножению нейтральный элемент 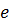 называется единичным
называется единичным
(или просто1), а симметричный элемент 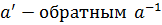
Утверждение. Для каждого элемента группы существует единственный симметричный элемент.
Доказывается от противного, с помощью ассоциативности.
 Пусть
Пусть 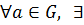 два симметричных ему элемента
два симметричных ему элемента 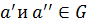 :
:
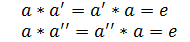

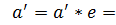
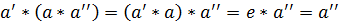
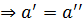

· Множество (K, 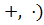 с двумя бинарными операциями
с двумя бинарными операциями 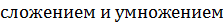 называется кольцом, если
называется кольцом, если
по сложению (I) множество (K, 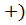 – абелева группа, а
– абелева группа, а
операция умножения (II) дистрибутивна относительно сложения (I).
Или более подробно
· Множество (K, 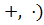 с двумя бинарными операциями
с двумя бинарными операциями 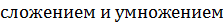 называется кольцом, если
называется кольцом, если
сложение
1) ассоциативно,
2) коммутативно,
3) 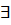 нейтральный элемент
нейтральный элемент 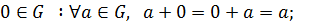
4) 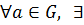 противоположный ему
противоположный ему 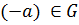 :
: 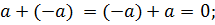
5) умножение 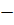 дистрибутивно относительно сложения.
дистрибутивно относительно сложения.
Требования 1-4 образуют аддитивную группу кольца
6) Если в кольце умножение ассоциативно, то такое кольцо называют ассоциативным.
7) Если в кольце умножение коммутативно, то такое кольцо называют коммутативным.
8) Если в кольце относительно умножения существует нейтральный элемент, то такое кольцо называют кольцом с единицей.
В кольце определены три операции: сложение, умножение и вычитание.
Примеры колец (Z, +, 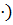 , (Q, +,
, (Q, +, 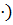 , (R, +,
, (R, +, 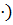 . Причем все кольца ассоциативные, коммутативные с единицей.
. Причем все кольца ассоциативные, коммутативные с единицей.
· Множество (П, +, 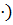 с двумя бинарными операциями сложением и умножением называется полем, если
с двумя бинарными операциями сложением и умножением называется полем, если
1) (П, +, 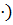 – ассоциативное, коммутативное кольцо с единицей, содержащее не менее двух элементов.
– ассоциативное, коммутативное кольцо с единицей, содержащее не менее двух элементов.
2) 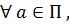 отличного нуля
отличного нуля 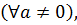
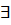 обратный элемент
обратный элемент 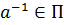 : относительно умножения
: относительно умножения 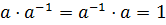
· Поле есть кольцо, в котором отличные от нуля элементы образуют коммутативную группу. Эта группа носит название мультипликативой группы поля.
В поле определены 4 операции: сложение, умножение, вычитание и деление.
Примеры полей (Q, +, 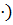 , (R, +,
, (R, +, 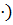
Поле комплексных чисел
Комплексным числом называется упорядоченная пара вещественных чисел.
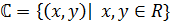
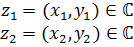 называются равными
называются равными 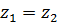
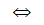
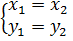
Введем две операции на множестве 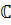 :
: 
(I) 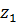 +
+ 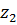 =
= 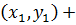
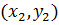 =(
=(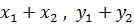 )
)
(II) 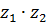 =
= 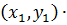
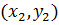 (
(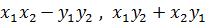 )
)
Можно доказать, что  ─ поле.
─ поле.






