Обзор некоторых основных алгебраических понятий
Алгебраические структуры. Множества. Алгебраические операции,
Предметом изучения современной алгебры являются алгебраические структуры.
· Под алгебраической структурой понимается множество, на котором определена система алгебраических операций, подчиняющихся аксиомам (законам) соответствующей структуры.
(Алгебраическая структура это множество с введенными операциями)
· Множеством в математике принято называть совокупность объектов произвольной природы, объединенных некоторым общим признаком, а сами объекты – элементами множества.
Обозначаются множества: A,B,C, …а их элементы: a,b,c,…
Знак принадлежности элемента а множеству А обозначается символом 
Одним из самых простых способов задать множество - дать полный список его элементов (применим к конечным множествам). Бесконечные множества задают путем указания характеристического свойства, т.е. свойства, которым обладают все элементы множества и только они. 
или 
Множество M - есть множество всех x, обладающих свойством P.
| 
|
| 
|
|
|
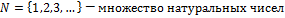
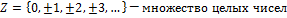
Для формулировки характеристических свойств, а также других утверждений, применяются сокращения: символ 
(квантор всеобщности); 
(
, а также другие символы 
и др.,
Пример,
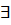n 
: 
(аксиома Архимеда)
Определим понятие алгебраической операции, обобщающее арифметические действия. Пусть E –произвольное непустое множество.
· Говорят, что на множестве Е задана бинарная алгебраическая операция 
если каждой упорядоченной паре 
однозначно поставлен в соответствие элемент 
: 
.
Note. Бинарная операция, это операция между двумя операндами. Обозначается: (Е, 
.
(тернарные, квартернарные)
Примеры бинарных операцией:
(R,+), (
, (
Для облегчения изучения множеств с операциями их классифицируют по свойствам операций.
Свойства бинарных операций
1). Коммутативность (возможность перестановки объектов) 
Чтобы применить алгебраическую операцию, определенную для двух элементов, к трем элементам нужно заключить в скобки либо два первых элемента, либо два последних.
2). Ассоциативность (возможность произвольного распределения скобок)
Операции сложение и умножение подчиняются законам коммутативности и ассоциативности на любом из множеств 
.
Для опровержения к-л свойства достаточно привести контр пример.
Требуется опровергнуть следующие утверждения:
| Утверждение | Контр пример |
( вычитание коммутативная операция
| 
|
| ( возведение в степень коммутативная операция
| 
|
( вычитание не коммутативная операция
( возведение в степень некоммутативная операция
