Структура общего решения ЛНДУ

Д У высших порядков

Как мы уже говорили, дифференциальные уравнения могут содержать производные различных порядков.

или .

Такие дифференциальные уравнения имеют решения, которые содержат столько произвольных постоянных интегрирования → каков порядок дифференциального уравнения, т.е. для дифференциального уравнения 2го порядка произвольных постоянных будет две С1 и С2, для 3го →С1,С2, и С3, и т.д.

Таким образом, общим решением (общим интегралом) такого дифференциального уравнения будет функция

Для получения частного решения, таких дифференциальных уравнений, необходимо задать столько начальных условий, каков порядок дифференциального уравнения, или сколько произвольных постоянных получено в общем решении.

Д У в полных дифференциалах. Интегрирующий множитель

Дифференциальное уравнение вида называется дифференциальным уравнением в полных диффернциалах, если его левая часть является полным дифференциалом некоторой гладкой функции 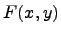, т.е. если , . Необходимое и достаточное условие для существования такой функции имеет вид:

Чтобы решить дифференциальное уравнение в полных дифференциалах необходимо найти функцию 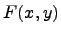. Тогда общее решение дифференциального уравнения можно записать в виде для произвольной постоянной С.

Интегрирующим множителем для дифференциального уравнения

называется такая функция , после умножения на которую дифференциальное уравнение превращается в уравнение в полных дифференциалах. Если функции M и N в уравнении имеют непрерывные частные производные и не обращаются в ноль одновременно, то интегрирующий множитель существует. Однако, общего метода для его отыскания не существует.

Структура общего решения ЛНДУ

Рассмотрим линейное неоднородное дифференциальное уравнение

+ (x) +... + (x)y' + (x)y = f(x).

Общим решением этого уравнения на отрезке [a;b] называется функция y = Φ(x, C1,..., Cn), зависящая от n произвольных постоянных C1,..., Cn и удовлетворяющая следующим условиям:

− при любых допустимых значениях постоянных C1,..., Cn функция y = Φ(x, C1,..., Cn) является решением уравнения на [a; b];

− какова бы ни была начальная точка (x0, y0, ), x0∈ [a;b], существуют такие значения C1 =C10,..., Cn = Cn0, что функция y = Φ(x, C10,..., Cn0) удовлетворяет начальным условиям y(x0) = y0, y '(x0) ,..., (x0) = .

Справедливо следующее утверждение (теорема о структуре общего решения линейного неоднородного уравнения).

Если все коэффициенты уравнения линейного однородного дифференциального уравнениния непрерывны на отрезке [a;b], а функции y1(x), y2(x),..., yn(x) образуют систему решений соответствующего однородного уравнения, то общее решение неоднородного уравнения имеет вид

y(x,C1,..., Cn) = C1 y1(x) + C2 y2(x) +... + Cn yn(x) + y*(x),

где C1,...,Cn — произвольные постоянные, y*(x) — частное решение неоднородного уравнения.

ЛНДУ 2-ого порядка

Линейные неоднородные дифференциальные уравнения второго порядка.

Уравнение вида y" + py' + qy = f(x), где р и q — вещественные числа, f(x) — непрерывная функция, называется линейным неоднородным уравнением второго порядка с постоянными коэффициентами.

Общее решение уравнения представляет собой сумму частного решения неоднородного уравнения н общего решения соответствующего однородного уравнения. Нахождение общего решения однородного уравнения изучено. Для нахождения частного решения воспользуемся методом неопределенных коэффициентов, не содержащим процесса интегрирования.

Рассмотрим различные виды правых частей уравнения y" + py' + qy = f(x).

1) Правая часть имеет вид F(x) = Pn(x), где Pn(х) – многочлен степени n. Тогда частное решение у можно искать в виде, где Qn (x) – многочлен той же степени, что и Pn (х), а r – число корней характеристического уравнения, равных нулю.

Пример. Найти общее решение уравнения у" – 2у' + у = x+1.

Решение: Общее решение соответствующего однородного уравнения имеет вид У = ех (C1 + C2x). Так как ни один из корней характеристического уравнения k2 – 2k + 1 = 0 не равен нулю (k1 = k2 = 1), то частное решение ищем в виде, где А и В – неизвестные коэффициенты. Дифференцируя дважды и подставляя, ' и " в данное уравнение, найдем –2А + Ах + В = х + 1.

Приравнивая коэффициенты при одинаковых степенях х в обеих частях равенства: А = 1, –2А + В = 1, – находим А = 1, В = 3. Итак, частное решение данного уравнения имеет вид = х + 3, а его общее решение у = еx (С1 + C2x) + х + З.

2) Правая часть имеет вид f(x) = eax Pn(x), где Рn (х) – многочлен степени n. Тогда частное решение следует искать в виде, где Qn(x) – многочлен той же степени, что и Рn (х), а r — число корней характеристического уравнения, равных а. Если а = 0, то f(х) = Рn (х), т. е. имеет место случай 1.

ЛОДУ с постоянными коэфф.

Рассмотрим дифференциальное уравнение

(8)

где – вещественные постоянные.

Для нахождения общего решения уравнения (8) поступаем так. Составляем характеристическое уравнение для уравнения (8): (9)

Пусть - корни уравнения (9), причем среди них могут быть и кратные. Возможны следующие случаи:

а) - вещественные и различные. Общим решением однородного уравнения будет ;

б) корни характеристического уравнения вещественные, но среди них есть кратные, т.е. , тогда общее решение будет

в) если корни характеристического уравнения комплексные (k=a±bi), то общее решение имеет вид .

Структура общ. решения ЛОДУ 2-ого порядка

Рассмотрим на [a; b] линейное однородное дифференциальное уравнение

+ (x) +... + (x)y' + (x)y = 0.

− при любых допустимых значениях постоянных C1,..., Cn функция y = Φ(x, C1,..., Cn) является решением уравнения на [a; b];

Справедливо следующее утверждение (теорема о структуре общего решения линейного однородного уравнения).

Если все коэффициенты уравнения линейного однородного дифференциального уравнениния непрерывны на отрезке [a;b], а функции y1(x), y2(x),..., yn(x) образуют систему решений этого уравнения, то общее решение уравнения имеет вид

y(x,C1,..., Cn) = C1 y1(x) + C2 y2(x) +... + Cn yn(x),

где C1,...,Cn — произвольные постоянные.