Структура общего решения однородного линейного ДУ.
Оно имеет вид A(x)y(n)+B(x)y(n-1)+…+K(x)y’+L(x)y=0
Для простоты запишем ЛОДУ в форме ЛОДУ второго порядка y’’+p(x)y’+q(x)y=0 (4)
Лемма 1. Если y0 – какое либо решение уравнения y’’+p(x)y’+q(x)y=0, а С – постоянная, то функция
Y=Cy0 также является решением ДУ (4).
Доказательство: надо подставить Y в левую часть (4). Так как Y’=Cy’0, то следовательно Y’’=Cy0’’
Результат подстановки будет таков Cy0’’=p(x) Cy’0+q(x) Cy0 или что тоже самое C[y0’’+ p(x)y’0+ q(x)y0]
Поскольку y0 решение (4), то Y’’+p(x)Y’+q(x)Y=0, что и доказывает Лемму 1.
Лемма 2. Если y1 и y2 – решения ДУ (4), то и сумма их Y= y1 и y2 так же является решением ДУ (4)
В результате получится Y’’+p(x)Y’+q(x)Y=0. Лемма 2 доказана.
Определение. Две функции y1 и y2 называются линейно независимыми, если их отношение не является постоянной величиной. Т.е. y1/ y2 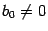 сonst.
сonst.
Основная теорема. Если y1 и y2 – два линейно независимых решения ДУ (4), то функция y=C1y1+C2y2, где C1 и C2 – произвольные постоянные, является общим решение уравнения (4).
Однородное ДУ второго порядка с постоянными коэффициентами имеет следующий вид:  , где
, где 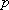 и
и  – константы (числа), а в правой части – строго ноль. Для того чтобы решить однородное ДУ 2 порядка, нужно составить так называемое характеристическое уравнение:
– константы (числа), а в правой части – строго ноль. Для того чтобы решить однородное ДУ 2 порядка, нужно составить так называемое характеристическое уравнение:  .
.
вместо второй производной записываем  ;
;
вместо первой производной записываем просто «лямбду»;
вместо функции у ничего не записываем.
1. Если характеристическое уравнение  – оно же обычное квадратное уравнение имеет два различных действительных корня
– оно же обычное квадратное уравнение имеет два различных действительных корня  и
и  (т.е., если дискриминант
(т.е., если дискриминант  ), то общее решение однородного уравнения выглядит так:
), то общее решение однородного уравнения выглядит так:  , где
, где  – константы.
– константы.
В случае если один из корней равен нулю, решение очевидным образом упрощается; пусть, например,  , тогда общее решение:
, тогда общее решение:  .
.
2. Если характеристическое уравнение имеет два кратных (совпавших) действительных корня  (дискриминант
(дискриминант  ),то общее решение однородного уравнения принимает вид:
),то общее решение однородного уравнения принимает вид:  , где
, где  – константы.
– константы.
Если оба корня равны нулю  , то общее решение опять же упрощается:
, то общее решение опять же упрощается:  . Кстати
. Кстати  является общим решением того самого примитивного уравнения
является общим решением того самого примитивного уравнения  .
.
3. Если характеристическое уравнение имеет сопряженные комплексные корня  и
и  (дискриминант
(дискриминант 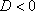 ), то общее решение однородного уравнения принимает вид:
), то общее решение однородного уравнения принимает вид:  , где
, где  – константы.
– константы.
Если получаются чисто мнимые сопряженные комплексные корни:  , то общее решение упрощается:
, то общее решение упрощается: 
Иногда встречаются нестандартные однородные уравнения, например уравнение в виде  , где при второй производной есть некоторая константа
, где при второй производной есть некоторая константа  , отличная от единицы (и, естественно, отличная от нуля). Алгоритм решения ничуть не меняется, следует невозмутимо составить характеристическое уравнение и найти его корни.
, отличная от единицы (и, естественно, отличная от нуля). Алгоритм решения ничуть не меняется, следует невозмутимо составить характеристическое уравнение и найти его корни.






