Дифференциальные уравнения высших порядков
Линейным дифференциальным уравнением n – го порядка называется уравнение вида F(x,y,y’,…,y(n))=0 здесь F(x,y,y’,…,y(n)) может на самом деле не зависеть от некоторых из величин x,y,y’,… Однако если уравнение именно n-го порядка, то F обязательно зависит от y(n).
Наиболее простым ДУ оказывается, когда оно имеет вид y(n)=f(x), где f(x) – заданная функция.
Общим решением ДУ n-го порядка называется функция: y=ф(x,C1,C2,…,Cn), существенно зависящая от n произвольных постоянных и обращающая уравнение: F(x,y,y’,…,y(n))=0 в тождество при любых значениях этих постоянных.
Решения, получаемые из общего при закреплении постоянных C1,C2,…,Cn, называются частными.
Замечание: например функция y=(C21+2C2+C3)x+C4+6C5 существенно зависит лишь от 2-х постоянных С’=C21+2C2+C3 и С’’=C4+6C5 и может быть записана в виде y=C’x+C’’
Случаи понижения порядка ДУ
Возьмём, например ДУ 2-го порядка, общий вид его будет таков F(x,y,y’,y’’)=0
Отметим некоторые его виды, когда его решение сводится к последовательному решению двух ДУ 1-го порядка.
1. Уравнение не содержит искомой функции y, т.е. имеет вид F(x,y’,y’’)=0
В этом случае надо ввести новую неизвестную функцию z, положив y’=z. Тогда y’’=z’ и =>
F(x,z,z’)=0 т.е. оказывается уравнением первого порядка относительно z.
Решив его найдём z=ф(x,C1), y’=ф(x,C1), а тогда y=Sф(x,С1)dx+С2
После замены 
может получиться уравнение с разделяющимися переменными, однородное уравнение первого порядка, а также некоторые другие интересности.
2. Когда уравнение не содержит независимой переменной x, т.е. имеет вид F(y,y’,y’’)=0
В данном уравнении в явном виде не участвует переменная х. Подстановка здесь более замысловата. Первую производную 
заменим некоторой пока еще неизвестной функцией 
, которая зависит от функции «игрек»: . Надо обратить внимание, что функция – это сложная функция. Внешняя функция – «зет», внутренняя функция – «игрек» («игрек» сам по себе является функцией).
Находим вторую производную. По правилу дифференцирования сложной функции: 
.
В принципе, можно запомнить данную замену формально и коротко: и 
Цель замены – опять же понизить порядок уравнения: Если – функция, зависящая от «игрек», то первая производная в дифференциалах расписывается так: 
. Далее разделяем переменные и интегрируем, после чего проведем обратную замену 
.
3. Когда уравнение имеет вид y’’=z(dz/dy), где z=y’x
Линейные дифференциальные уравнения высших порядков
Линейным ДУ любого порядка называется такое ДУ, в которое неизвестные элементы y,y’,y’’,… входят в первых степенях, не перемножаясь между собой. Иными словами, это уравнение вида
A(x)y(n)+B(x)y(n-1)+…+K(x)y’+L(x)y=M(x) где A(x), B(x)…K(x), L(x), M(x) –заданые функции от х или постоянные величины, причем A(x)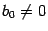 
0 и уравнение можно разделить на A(x), что приводит его к виду y(n)+b(x)y(n-1)+…..+k(x)y’+l(x)y=m(x), где положено b(x)=B(x)/A(x),…..,m(x)=M(x)/A(x)
Функция m(x) – называется свободным членом уравнения. Если m(x)=0, то уравнение называется однородным. Если же m(x) 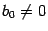0, то уравнение называется неоднородное, если все коэффициенты A(x), B(x)…K(x), L(x) – постоянные числа, то уравнение называется линейным дифференциальным уравнением высшего порядка с постоянными коэффициентами.
