Тело, коэффициент поглощения которого меньше единицы и не зависит от длины волны света, падающего на него, на­зывают серым

Серых тел в природе нет, однако некоторые тела в определен­ном интервале длин волн излучают и поглощают как серые. Так, например, тело человека иногда считают серым, имеющим коэф­фициент поглощения приблизительно 0,9 для инфракрасной об­ласти спектра.

 

§ 22.2. Закон Кирхгофа

Между спектральной плотностью энергетической светимости и монохроматическим коэффициентом поглощения тел существует определенная связь, которую можно пояснить на следующем при­мере.

В замкнутой адиабатной оболочке находятся два разных тела в условиях термодинамического равновесия, при этом их темпера­туры одинаковы. Так как состояние тел не изменяется, то каждое из них излучает и поглощает одинаковую энергию. Спектр излу­чения каждого тела должен совпадать со спектром электромаг­нитных волн, поглощаемых им, иначе нарушилось бы термодина­мическое равновесие. Это означает, что если одно из тел излучает какие-либо волны, например красные, больше, чем другое, то оно должно больше их и поглощать.

Количественная связь между излучением и поглощением была установлена Г.Кирхгофом в 1859 г.: при одинаковой температу­ре отношение спектральной плотности энергетической свети­мости к монохроматическому коэффициенту поглощения одина­ково для любых тел, в том числе и для черных (закон Кирх­гофа):

(22.4)

где — спектральная плотность энергетической светимости чер­ного тела (индексы у скобок означают тела 1, 2 и т. д.). Закон Кирхгофа может быть записан и в таком виде:

(22.5)

Отношение спектральной плотности энергетической светимос­ти любого тела к его соответствующему монохроматическому ко­эффициенту поглощения равно спектральной плотности энергети­ческой светимости черного тела при той же температуре.

Из (22.5) находим еще одно выражение:

(22.6)

Так как для любого тела (нечерного) , то, как следует из (22.6), спектральная плотность энергетической светимости любо­го тела меньше спектральной плотности энергетической свети­мости черного тела при той же температуре. Черное тело при про­чих равных условиях является наиболее интенсивным источни­ком теплового излучения.

Из (22.6) видно, что если тело не поглощает какое-либо излуче­ние , то оно его и не излучает

Пользуясь законом Кирхгофа (22.6) и зная из эксперимента спектр излучения черного тела , а также зависимость монохроматического коэффициента поглощения тела от длины вол­ны 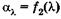, можно в соответствии с (22.6) найти спектр излуче­ния тела

 

 

§ 22.3. Законы излучения черного тела

Излучение черного тела имеет сплошной спектр. Графики спектров излучения для разных температур приведены на рис. 22.2. Из этих экспериментальных кривых можно сделать ряд вы­водов.

Существует максимум спектральной плотности энергетиче­ской светимости, который с повышением температуры смещается в сторону коротких волн.

На основании (22.2) энергетическую светимость черного тела R_е⁰ можно найти как площадь, ограниченную кривой и осью абс­цисс, или

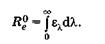(22.7)

Из рис. 22.2 видно, что энергетическая светимость увеличива­ется по мере нагревания черного тела.

Долгое время не могли получить теоретически зависимость спектральной плотности энергетической светимости черного тела от длины волны и температуры, которая отвечала бы эксперимен­ту. В 1900 г. это было сделано М. Планком.

В классической физике испускание и поглощение излучения те­лом рассматривались как непрерывный волновой процесс. Планк пришел к выводу, что именно эти основные положения не позволя­ют получить правильную зависимость. Он высказал гипотезу, из которой следовало, что черное тело излучает и поглощает энергию не непрерывно, а определенными дискретными порциями — кван­тами. Представляя излучающее тело как совокупность осциллято­ров, энергия которых может изменяться лишь на величину, крат ную кванту энергии hv =hc/l, Планк получил формулы

(22.8 а)

(22.8 6)

(h = 6,626176 • 10 ^-34 Дж • с — посто­янная Планка, с — скорость света в ва­кууме, k— постоянная Больцмана),

которые прекрасно описывают экспериментальные данные, в част­ности кривые, изображенные на рис. 22.2.

На основании (22.6) и (22.8 а) спектр излучения серого тела мо­жет быть выражен зависимостью

(22.9)

где а — коэффициент поглощения серого тела.

Из формулы (22.8) можно получить расчетным путем законы, которые были установлены экспериментально еще до основопола­гающей работы Планка. Рассчитаем энергетическую светимость черного тела по формуле (22.7) с учетом (22.8):

Произведя замену переменных , запишем

(22.9а)

Без вывода укажем, что 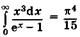. Множитель при Г⁴ в (22.9а),

состоящий из постоянных величин, равен

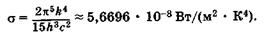(22.10)

Окончательно получаем

(22.11)

Это закон Стефана—Больцмана: энергетическая светимость черного тела пропорциональна четвертой степени его термоди­намической температуры. Величину а называют постоянной Стефана — Больцмана.

Для серых тел [см. (22.2) и (22.9)] имеем

(22.12)

Закон Стефана—Больцмана можно качественно проиллюстри­ровать на разных телах (печь, электроплита, металлическая бол­ванка и т. д.): по мере их нагревания ощущается все более интен­сивное излучение.

Функция , записанная в виде (22.8 а), имеет экстремум при услввии

(22.13)

Отсюда получаем закон смещения Вина (см. рис. 22.2):

(22.14)

где — длина волны, на которую приходится максимум спек­тральной плотности энергетической светимости черного тела, b = = 0,28978 • 10 ^-2 м • К — постоянная Вина. Этот закон выполня­ется и для серых тел.

Проявление закона Вина известно из обыденных наблюдений. При комнатной температуре тепловое излучение тел в основном при­ходится на инфракрасную область и человеческим глазом не воспри­нимается. Если температура повышается, то тела начинают светить­ся темно-красным светом, а при очень высокой температуре — бе­лым с голубоватым оттенком, возрастает ощущение нагретости тела.

Законы Стефана—Больцмана и Вина позволяют, регистрируя излучение тел, определять их температуры (оптическая пиро­метрия).

 

§ 22.4. Излучение Солнца. Источники теплового излучения, применяемые для лечебных целей

Наиболее мощным источником теплового излучения, обуслов­ливающим жизнь на Земле, является Солнце.