I:
S: Качество построенной модели парной регрессии может быть измерено:
-: t-критерием Стьюдента
+: коэффициентом детерминации
-: коэффициентом корреляции
-: F-критерием Фишера
I:
S: Коэффициент детерминации для модели линейной парной регрессии может быть рассчитан по формуле:
-:
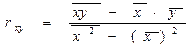 |
+: R=(rxy)2
-:
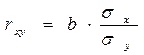 |
I:
S: Линейный коэффициент детерминации R может принимать значения в диапазоне:
-: (-1; 1)
+: [0; 1]
-: [-1; 1]
-: [-1.1; 1]
I:
S: Линейный коэффициент детерминации R не может принимать значения в диапазоне:
+: (1; 1.5)
-: [0; 1]
-: [0; 0.99]
-: [0.1; 1]
I:
S: Линейный коэффициент детерминации R может принимать значения в диапазоне:
-: (-1; 1)
-: [0; 1.5]
+: [0; 1]
-: [-1.1; 1]
I:
S: Линейный коэффициент детерминации R может принимать значения в диапазоне:
+: [0; 1]
-: [0; 1.1]
-: [-1; 1]
-: [-0.5; 1]
I:
S: Линейный коэффициент детерминации R может принимать значения только в диапазоне:
-: [-1; 1]
-: [-1.1; 1]
-: [-1; 1]
+: [0; 1]
I:
S: Линейный коэффициент детерминации R не может принимать значение равное:
-: 0.5
-: 0.99
+: -0.5
-: 1
I:
S: Линейный коэффициент детерминации R не может принимать значение равное:
-: 0.5
-: 0.99
+: 1.05
-: 1
I:
S: Линейный коэффициент детерминации R не может принимать значение равное:
-: 0.6
-: 0.01
+: -1.05
-: 1
I:
S: Линейный коэффициент детерминации R может принимать только значение равное:
-: -0.5
+: 0.99
-: 1.05
-: 1.2
I:
S: Линейный коэффициент детерминации R может принимать только значение равное:
+: 0.35
-: -0.99
-: 1.05
-: 1.001
I:
S: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= -0.5
-: 0.5
+: 0.25
-: -0.5
-: -0.25
I:
S: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= -0.3
-: 0.3
+: 0.09
-: -0.3
-: -0.09
I:
S: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= -0.4
-: 0.4
+: 0.16
-: -0.4
-: -0.16
I:
S: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= -0.25
+: 0.0625
-: -0.625
-: 0.5
-: -0.25
I:
S: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= -0.6
+: 0.36
-: -0.36
-: 0.6
-: -0.24
I:
S: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= -0.7
-: 0.07
-: -0.49
+: 0.49
-: -0.7
I:
S: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= 0.7
-: 0.07
-: -0.49
+: 0.49
-: -0.7
I:
S: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= 0.8
+: 0.64
-: -0.64
-: 0.8
-: -0.8
I:
S: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= 0.9
-: -0.81
+: 0.81
-: 0.9
-: -0.9
I:
S: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= 0.65
-: -0.65
-: 0.65
+: 0.4225
-: -0.125






