Существуют ь 2 метода формирования выборочной совокупности.
1. Применение повторного отбора
2. Применение бесповторного отбора
В первом случае отобранный в выборку элемент возвращается в генеральную совокупность и может попасть в выборку вновь.
Во втором случае отобранные в выборку элементы в генеральную совокупность не возвращаются, и следовательно, не могут попасть в выборку вновь.
Существует 5 видов формирования выборочной совокупности:
1. Собственно - случайная выборка
2. Механическая выборка
3. Типическая выборка
4. Серийная выборка
5. Комбинированная выборка
Собственно – случайная выборка.
Отбор единиц из. генеральной совокупности в выборочную производится случайным образом – наугад, без какой – либо систематизации элементов генеральной совокупности. Для этой цели используется компьютерный датчик случайных чисел.
Механическая выборка.
Совокупность сначала упорядочивается по определённому признаку (например,алфавитному) и затем из этой упорядоченной последовательности выбираются единицы через равные промежутки, т.е. используется некоторая регулярная процедура, а начальный элемент выбирается случайным образом.
Типическая выборка (стратифицированная, районированная)
Генеральная совокупность предварительно разбивается на отдельные группы однотипных элементов, и затем из каждой группы случайным или иным способом отбираются единицы пропорционально удельному весу каждой группы.
Серийная выборка.
В отличии от предыдущих способов, когда выбираются отдельные единичные элементы, в выборку отбираются группы единиц одинаковой численности, и затем в каждой группе проводится сплошное обследование.
Комбинированная выборка.
Применяются различные виды выборки в различных сочетаниях.
3.Расчёт средней и предельной ошибок выборки
Применение выборочного метода наблюдения связано с измерением степени достоверности статистических характеристик генеральной совокупности, полученных по результатам выборочного наблюдения. Достоверность генеральных параметров зависит от репрезентативности выборки, т.е. от того, насколько полно и адекватно представлены в выборке статистические свойства генеральной совокупности.
Как правило, статистические характеристики выборочной и генеральной совокупностей не совпадают, а отклоняются на некоторую величину ε, которую называют ошибкой выборки(ошибкой репрезентативности).
Ошибка выборки – это разность между значением показателя, которое было получено по выборке, и генеральным значением этого показателя. Например, разность
= | 
- 
|
определяет ошибку репрезентативности для средней величины признака.
Формирование выборок происходит случайным образом, поэтому все получаемые значения выборочных показателей также являются случайными и могут принимать для разных выборок из одной и той же генеральной совокупности разные значения. Например, если из генеральной совокупности сформировать 3 выборки, то средние величины каждой из этих выборок не совпадут:
х1≠ х2 ≠ х3
Поскольку значения выборочных показателей случайны, то и ошибки выборки также случайны. Ввиду этого в статистике рассматриваются 2 вида ошибок выборки - средняя ( обозначение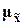 
) и предельная (обозначение ∆ 
).
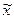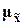1. Для среднего значения признака средняя ошибка выборки (ее называют также стандартной ошибкой) выражает численное значение среднего квадратического отклонения s выборочной средней от математического ожидания M[ ] генеральной средней :.
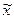| | – М [ 
]|
Для определения 
существуют специальные формулы. В табл.7.2 приведены формулы для собственно-случайной и механической выборок (они одинаковы).
| Выборка | Отбор | Средняя 
| Доля, w |
| Собствен-но случай-ная и механи-ческая | Повторный отбор | 
| 
|
| Бесповтор-ный отбор | 
| 
| |
| Типиче-ская | Повторный отбор |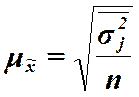 
| |
| Бесповтор-ный отбор | 
| ||
| Серий-ная выборка | Повторный отбор | 
| |
| Бесповтор-ный отбор |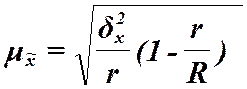 
|
Как видно из этих формул, величина средней ошибки 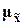зависит от объема выборки n и от величины вариации признака s: чем больше n и меньше s, тем меньшеошибка .
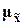2. Предельная ошибка выборки 
определяет границы интервала, в пределах которого будет находиться генеральная средняя :
.
(•)
- ∆ +∆
_
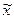
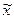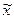
Эти границы задают так называемый доверительный интервал генеральной средней – случайную область значений признака,, которая с вероятностью P (близкой к 1) гарантированно содержит значение генеральной средней. Эту вероятность называют доверительной вероятностью ( или уровнем надежности, если она выражается в процентах).
Известно, что 0 ≤ Р ≤ 1. Наиболее часто в экономических расчетах используются следующие значения Р:
P=0,683;
P=0,954;
P=0,997.
В математической статистике доказано, что предельная ошибка выборки кратна средней ошибке 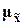с коэффициентом кратности t, зависящим от значения доверительной вероятности P:
(1)
Величина коэффициента t (называемого также коэффициентом доверия) является нормированным отклонением, которое вычисляется по формуле
t =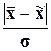 
и выражается не в натуральных единицах, а в сигмах: 1σ, 2σ, 3σ и т.д.
Рассчитаны специальные таблицы, связывающие доверительные вероятности Р и коэффициенты кратности t ( таблицы интегральной функции Лапласа). Для вышеприведенных уровней надежности P коэффициенты доверия задаются следующей таблицей:
| Р | 0,683 | 0,954 | 0,997 |
| t |
Например, если t=2, то с вероятностью P=0,954 можно утверждать, что расхождение между выборочной и генеральной средними | - | не превысит двукратной величины средней ошибки выборки:
= | - 
| 
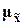
Таким образом, предельная ошибка выборки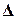 
позволяет определить предельные значения показателей генеральной совокупности и их доверительные интервалы. Для генеральной средней предельные значения и доверительные интервалы определяются выражениями:
,
(2)
Аналогично для доли р имеют место выражения
p = w ± ∆w
w - ∆w ≤p ≤ w + ∆w (3)
Что касается величины дисперсии генеральной совокупности σ2N, то она может быть оценена непосредственно по выборочной дисперсии σ2n.
В математической статистике доказано, что при малом числе наблюдений (особенно при n 
40-50)для вычисления генеральной дисперсии σ2N по выборочной дисперсии σ2n следует использовать формулу
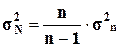(4)
При достаточно больших n значение поправочного коэффициента 
близко к 1 (при n=100его значение равно 1,101, а при n=500- 1,002 и т.д.). Поэтому при достаточно больших n можно приближено считать, что обе дисперсии совпадают:
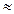σ2N 
σ2n.
Задача. (3-е задание по курсовой работе)
Для определения среднего срока пользования краткосрочным кредитом в банке была произведена 5%- ная механическая выборка в которую попало 100 счетов. В результате исследования этих счетов установлено, что средний срок пользования кредитом составляет 30 дней при среднем квадратическом отклонении 9 дней.
В 5- ти счетах из 100 срок пользования кредитом превысил 60 дней.
Необходимо с вероятностью 0,954 определить:
1) пределы, в которых будет находиться срок пользования долгосрочным кредитом по банку в целом, т.е. в генеральной совокупности,
2) долю счетов со сроком пользования кредитом более 60 дней.
Решение.
Прежде всего необходимо текстовую постановку задачи преобразовать в числовой формат, введя параметры, необходимые для использования расчетных формул табл.7.2.
n = 100 т.к. в выборку попало 100 счетов
N = 2000 счетов т.к. выборка 5%-ая
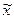= 30 дней
s = 9 дней среднее отклонение от среднего срока пользования кредитом
Р = 0,954 
t = 2
w = 0,05 поскольку в 5-ти случаев из 100 срок в 30 дней превышен:
-
1) Применим формулу расчета средней для бесповторной выборки из табл.7.2
=
Следовательно, согласно формуле (1)
=2 * =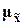
Применив формулу (2), получаем
т.е. средняя будет лежать в пределах
2) Для расчёта среднего срока превышения кредита более чем на 60 дней по банку в целом используем соответствующую формулу из табл.7.2
Следовательно, согласно формуле (1)
∆w =2 *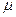 
w =
Применив формулу (3), получаем
5% - 4,2%≤ p ≤ 5% + 4,2%,
Следовательно, генеральная доля p будет лежать в пределах
0,8% ≤ р ≤ 9,2%
4. Определение необходимого объёма выборки
При планировании выборочного обследования необходимо находить объём выборки такой, чтобы была обеспечена заданная надёжность расчётов.
Существуют формулы для определения необходимого объёма выборки. Для собственно-случайной и механической выборки эти формулы имеют вид:
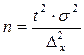- для повторной выборки
- для бесповторной выборки
Пример.
В районе проживают 2000 семей. Необходимо провести выборочное обследование методом случайного бесповторного отбора для нахождения среднего размера семьи.
Определить необходимый объём выборки при условии, что с вероятностью 0,954 ошибка выборки не должны превышать 1 человека при среднем квадратичном отклонении 3 человека.
Условие задачи в числовых параметрах:
N = 2000 человек
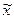∆ = 1 человек
s = 3 человека
Р = 0,954 t = 2
Решение.
семей
Вывод: Из 2000 семей для обследования с заданной степенью надежности нужно отобрать 35 семей.
