Тема 6.
СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВАРИАЦИИ
В РЯДАХ РАСПРЕДЕЛЕНИЯ.
Понятие вариации признака в совокупности.
Система показателей вариации.
Правило сложения дисперсий и его применение.
Виды дисперсий. Правило сложения дисперсий.
3.2 Расчёт показателей тесноты и силы связи признаков на основе правила сложения дисперсий.
Характеристика формы распределения единиц совокупности.
Понятие вариации признака в совокупности.
Информации о средних значениях обычно бывает недостаточным для полного анализа изучаемого процесса (явления), т.к. иногда совершенно разные по внутреннему строению совокупности могут иметь равные средние величины
Пример.
5 5
_
Ряд 1. 95 100 105 хi = 100
_
Ряд 2. 75 100 125 х2 = 100
25 25
Эти два ряда имеют одинаковую среднюю, однако расхождения между вариантами 2-го ряда в 5 раз больше чем между вариантами 1-го ряда, т.е. ряды качественно разные.
Следовательно, при изучении совокупностей необходимо учитывать разброс значений признака единиц совокупности относительно средней величины, т.е. вариацию (колеблемость) признака.
Вариации – это различие индивидуальных значений признака в ряде распределения. Вариация возникает в виду того, что на объект действуют не только систематические, но и случайные факторы.
При оценке вариации необходимо учитывать разность  , т.е. отклонение индивидуального варианта
, т.е. отклонение индивидуального варианта  от среднего значения
от среднего значения  .Затем
.Затем
можно рассчитать среднее из этих отклонений и рассматривать эту величину как один из показателей вариации признака.
Если вариация (т.е. разброс значений признака вокруг их средней величины) незначительна, то средняя величина типична для данной совокупности.
Если вариация велика (т.е. отклонения значений признака от средней) значительны, то средняя является ненадёжной х арактеристикой совокупности.
Для измерения вариация служит специальная система показателей, которые позволяют определить величину разброса значений признака (и тем самым установить надёжность средней).
Кроме того, эти показатели позволяют:
· Определить предельные границы изменения признака
· Установить, является лисовокупность однородной
· Установить тесноту и силу взаимосвязи между факторными признаками и результативным признаком.
СИСТЕМА ПОКАЗАТЕЛЕЙ ВАРИАЦИЙ.
Показатели вариации (колеблемости) признакаоценивают степень (разброса) рассеяния вариантов значений признака относительно своего центра 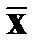 (или Ме).
(или Ме).
Различают показатели размера вариации (абсолютные) и интенсивности вариации (относительные).
1.Показатели размера вариации
· размах вари ации, устанавливающий предельное значение амплитуды колебаний признака;
R = xmax - xmin (1)
· среднее линейное отклонение 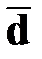 , вычисляемое как среднее арифметическое из абсолютных отклонений | xi -
, вычисляемое как среднее арифметическое из абсолютных отклонений | xi - 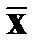 |:
|:
 (2)
(2)
· дисперсия s2 (или D), рассчитываемая как среднее арифметическое из квадратов отклонений (xi - 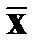 ):
):
 (3)
(3)
· среднее квадратическое (стандартное) отклонение s, вычисляемое как корень квадратный из дисперсии s2:
 (4)
(4)
Эти формулы применяются, когда изучается вариация в дискретных рядах распределения, без учёта частот.
Если анализируется вариация в интервальных рядах, то используется взвешенная форма показателей вариации:
 (5)
(5)
 (6)
(6)
 (7)
(7)
Для расчёта дисперсии существует удобная формула для вычислений:
 (8)
(8)

Показатели R, 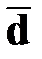 и s являются величинами именованными и выражаются в тех же единицах, что и изучаемый признак. Дисперсия s2 считается безразмерной величиной
и s являются величинами именованными и выражаются в тех же единицах, что и изучаемый признак. Дисперсия s2 считается безразмерной величиной
В статистической практике для оценки вариации наиболее широко применяются показатели s2 и s. Они основаны на учете отклонений (xi - 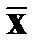 ) индивидуальных значений признака xi от средней арифметической
) индивидуальных значений признака xi от средней арифметической 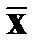 и являются обобщающими характеристиками различия в значениях признака.
и являются обобщающими характеристиками различия в значениях признака.
Среднее квадратическое отклонение s показывает, на сколько в среднем отклоняются индивидуальные значения признака xi от их средней величины 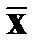 .
.
Размерность отклонения s совпадает с размерностью самого признака, поэтому этот показатель экономически хорошо интерпретируется. Отклонения, выраженные в s, принято считать стандартными.
Дисперсия s2 оценивает средний квадрат отклонений (xi - 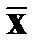 ). Величина s очень чутко реагирует на вариацию признака (за счет возведения отклонений в квадрат) и органически вписывается в аппарат математической статистики (дисперсионный, корреляционный анализ и др.). На расчете дисперсии основаны многие статистические показатели.
). Величина s очень чутко реагирует на вариацию признака (за счет возведения отклонений в квадрат) и органически вписывается в аппарат математической статистики (дисперсионный, корреляционный анализ и др.). На расчете дисперсии основаны многие статистические показатели.
2.Показатели интенсивности вариации признака.
Это относительные показатели, измеряемые, как правило, в процентах:
Vs=  , Vd=
, Vd= 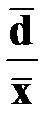 , VR=
, VR=  , VMe=
, VMe=  .
.
Среди показателей интенсивности вариации наиболее часто применяется коэффициент вариации Vs, который выражается в процентах и вычисляется по формуле
 (9)
(9)
Величина Vs оценивает интенсивность колебаний вариантов относительно их средней величины.
Принята следующая оценочная шкала колеблемости признака:
0%<Vs  40% - колеблемость незначительная;
40% - колеблемость незначительная;
40%< Vs  60% - колеблемость средняя (умеренная); (10)
60% - колеблемость средняя (умеренная); (10)
Vs>60% - колеблемость значительная.
Для нормальных и близких к нормальному распределений показатель Vs служит индикатором однородности совокупности: принято считать, что при выполнимости неравенства
Vs  33% (11)
33% (11)
совокупность является количественно однородной по данному признаку.
Коэффициент вариации Vs часто используется для сравнения колеблемости признаков в различных рядах распределения, когда сравнивается вариация разных признаков в одной и той же совокупности или же вариация одного и того же признака в различных совокупностях, имеющих разные средние 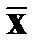 .
.
Пример.
Имеется ряд распределения (табл.6.1) сотрудников по стажу работ.
Таблица 6.1






