В рассмотренной выше классической модели управления запасами Уилсона товар поставляется либо мгновенно, либо в строго установленный отрезок времени, т.е. не предусматриваются сбои в поставке заказа и не допускается дефицит. Данное условие на практике зачастую не выполняется, что ограничивает применение модели. Решение этой проблемы рассматривается в модели управления запасами с фиксированным размером заказа.
Разобьем ось объема запаса на графике зависимости «объем запаса – время» на три части (рис. 1.2.1).
 |
Рис.1.2.1. Графическое отображение модели управления запасами с фиксированным размером заказа: I – объем запаса в момент поставки, соответствующий минимальным затратам, связанным с доставкой и хранением товара; II – уровень запаса, расходуемый за время поставки; III – уровень запаса, покрывающий потребность в товаре в случае задержки в поставке
Первая часть определяет минимальное и максимальное значение запасов в момент поставки, удовлетворяющее условию минимизации затрат, связанных с доставкой и хранением товаров; вторая – объем запаса, который расходуется за время поставки; третья – уровень запаса, обеспечивающий удовлетворение в товаре в случае задержки в поставке. Графически такую модель представим на рисунке 1.2.2.
 |
Рис.1.2.2. Графическая модель управления запасами с фиксированным размером заказа, в случае отсутствия сбоев в поставках: Максимально возможный объем запаса – максимальный уровень запаса в момент поставки; Пороговый уровень – наименьший объем запасов в момент поставки; Страховой запас – уровень запаса, покрывающий потребность в товаре в случае задержки в поставке
В данной модели подача заказа производится в день достижения объема запасов, хранимых на складе, порогового уровня.
В случае разовых сбоев в поставках потребность в товаре будет покрываться за счет страхового запаса (рис. 1.2.3), поэтому в момент поставки уровень запаса будет ниже порогового уровня. Восполнение запасов до порогового уровня может быть осуществлено за счет разовой корректировки времени подачи заказа.
Рис.1.2.3. Графическое представление модели управления запасами в случае разовых сбоев в поставке
При многократных сбоях в поставке может наступить дефицит в товарах (рис. 1.2.4), что является недопустимым в данной модели. Для предотвращения появления дефицита на складе, в случае если нельзя выбрать нового поставщика, необходимо изменить время размещения заказа.
 |
Рис.1.2.4. Графическая модель управления запасами с фиксированным размером заказа в случае многократной задержки в поставке
Определение основных параметров модели (страховой запас, пороговый уровень, максимально возможный объем запаса) удобно вести в табличной (табл. 1.2.1) форме.
Определение параметров модели управления запасами
с фиксированным размером заказа
Таблица 1.2.1
| Показатель | Формула для расчета |
| Оптимальный размер заказа Q*, шт | 
|
| Ожидаемое дневное потребление, шт./дн. | Потребность / количество рабочих дней |
| Время расходования заказа, дн. | Оптимальный размер заказа / ожидаемое дневное потребление |
| Потребление за время поставки, шт. | Время поставки * ожидаемое дневное потребление |
| Максимальное потребление за время поставки, шт. | (Время поставки + задержка в поставке) * ожидаемое дневное потребление |
| Страховой запас, шт. | Задержка в поставке * ожидаемое дневное потребление |
| Пороговый уровень, шт. | Страховой запас + потребление за время поставки |
| Максимально желательный уровень запаса, шт. | Страховой запас + оптимальный размер заказа |
Задача
Стоимость поставки комплектующих для мягкой мебели составляет 300 руб. Годовая потребность в комплектующих – 2100 штук. Стоимость хранения материалов на складе равна 700 руб./год. Время поставки товаров – четыре дня, максимальное время задержки в поставке – два дня. Определить оптимальный размер заказа, рассчитать основные параметры модели управления запасами с фиксированным размером заказа и показать графически реализацию модели для следующих ситуаций: отсутствие сбоев в поставках, однократная задержка, многократные задержки.
Решение
Для определения оптимального размера заказа рассчитаем суточную потребность и суточную стоимость хранения товара.
Суточная потребность в комплектующих:
,
где
Sгод – годовая потребность в комплектующих, шт.;
n – количество рабочих дней в году (226 дней), дн.
шт.
Суточная стоимость хранения комплектующих:
,
где
Wгод – годовая стоимость хранения комплектующих, руб./год.;
n – количество рабочих дней в году (226 дней), дн.
руб./сут.
Определение основных параметров модели (страховой запас, пороговый уровень, максимально возможный объем запаса) будем вести в табличной форме.
Определение параметров модели управления запасами
с фиксированным размером заказа
Таблица 1.2.2
| Показатель | Формула для расчета |
| Оптимальный размер заказа, шт. |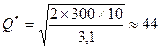 
|
| Ожидаемое дневное потребление, шт./дн. | 
|
| Время расходования заказа, дн. | 
|
| Потребление за время поставки, шт. | 
|
| Максимальное потребление за время поставки, шт. | 
|
| Страховой запас, шт. | 
|
| Пороговый уровень, шт. | 
|
| Максимально желательный уровень запаса, шт. | 20+44=64 |
Графически модель управления запасами с фиксированным размером заказа в случае отсутствия сбоев в поставках представлена на рис. 1.2.5.
Рис.1.2.5. Графическая модель управления запасами с фиксированным размером заказа в случае отсутствия сбоев в поставках
В качестве исходного объема запасов, хранимого на складе, выбран максимально возможный объем, рассчитанный в модели. Заказ производится в момент достижения порогового уровня запасов.
Рис.1.2.6. Графическая модель управления запасами с фиксированным размером заказа в случае разовых сбоев в поставке
Если происходит однократная задержка в поставке, равная двум дням, то полностью расходуется страховой запас (7-й день), и объем товара в момент поставки (44 шт.) окажется ниже порогового уровня (рис. 1.2.6). Для восполнения запасов до максимально возможного уровня необходимо определить день размещения заказа, чтобы поставка товара произошла в день достижения запасов страхового уровня.
Так как в момент поставки объем запасов на складе равен 44 штукам, то день, когда объем запасов достигнет порогового уровня (20 шт.), определяется следующим образом:
Итого получим, что на десятый день (7+3) объем запасов, хранимых на складе, достигнет порогового уровня. Определим объем запасов, при котором необходимо сделать заказ.
Сначала определим количество целых циклов n, проходящих за время поставки tц:
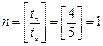
Число дней L, на которое время поставки превышает количество полных циклов расходования запаса:
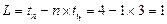день.
Таким образом, размещение заказа необходимо произвести на 6-й день для поставки товара на 10-й день, т.е. за 1 день до полного израсходования запасов на складе (рис. 1.2.6). Объем запаса, при котором необходимо сделать заказ (6-й день), равен L*S = 1*10 = 10 шт.
При неоднократных задержках в поставке для недопущения дефицита в товарах необходимо скорректировать время размещения заказа. Если произошла задержка в поставке, равная двум дням, то объем запасов на складе, при котором размещается заказ, равен 10 шт. (расчет в случае однократной задержки в поставке).
 |
Рис.1.2.7. Графическая модель управления запасами с фиксированным размером заказа при неоднократных задержках в поставках
Если повторно произошла задержка в поставке равная двум дням, то модель управления запасами не перейдет в дефицитное состояние (рис. 1.2.7).В данном случае заказ, равный 44 штукам, необходимо размещать при достижении объема товаров на складе 10 шт., за один день до поставки.
