Зависимость между числовыми значениями случайной величины и вероятностью их появления устанавливается законом распределения вероятностей случайных величин. Закон распределения вероятностей дискретной случайной величины можно представить в виде таблицы или графика, показывающего, с какой вероятностью случайная величина X принимает то или иное числовое значение xi.
Закон распределения вероятностей непрерывной случайной величины, которая может принимать любое значение в пределах заданного интервала нельзя представить в виде таблицы.
Закон распределения представляют в виде дифференциальной функции распределения или плотности распределения вероятности pX (x). Эта функция представляет собой предел отношения вероятности того, что случайная величина X примет значение, лежащее в интервале от x до х +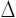 
x, к величине интервала 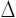х, при 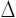х, стремящемся к нулю.
Характер рассеяния достаточно большой совокупности значений случайной величины, как правило, соответствует определённому теоретическому закону распределения.
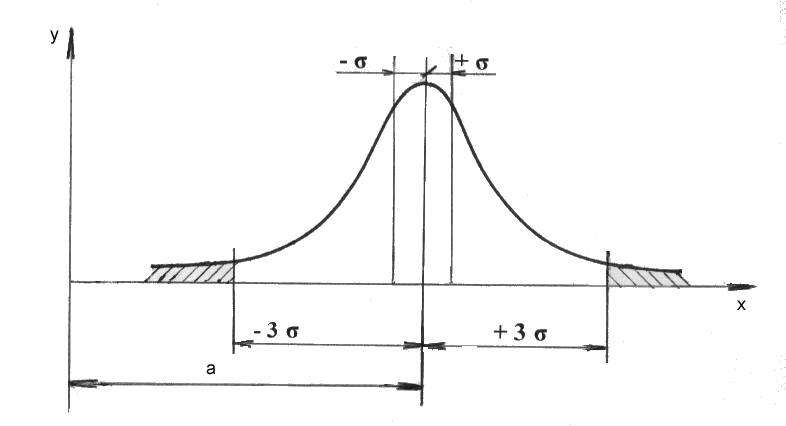Рассеяние значений случайной величины, изменение которой зависит от большого числа факторов, когда ни один из факторов не имеет преобладающего влияния, подчиняется закону нормального распределения вероятностей (закону Гаусса), показанного на рис 3.3.
Этому закону с некоторым приближением может подчиняться: рассеяние погрешностей многократных измерений; рассеяние погрешностей изготовления; погрешности измерения линейных и угловых размеров; массы деталей; величин твердости и других механических и физических величин.
Закон нормального распределения имеет следующие свойства:
· вероятность появления положительных и отрицательных погрешностей одинакова;
· малые по величине погрешности имеют большую вероятность появления, чем большие;
· алгебраическая сумма отклонений от среднего значения равна нулю.
Зависимость плотности вероятности определяется уравнением:
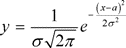(3.2) где a и 
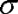- параметры распределения; x - аргумент функции плотности вероятности, т.е. случайная величина, изменяющаяся в пределах - 
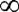< x < + 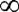; e - основание натуральных логарифмов. Нормальное распределение представляет собой кривую симметричную относительно оси ординат. Величина a равна математическому ожиданию MX случайной величины X, определяемому по формулам:
для дискретной величины
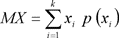(3.3), где xi - возможное значение дискретной случайной величины; p (xi) - вероятность значения xi дискретной случайной величины;
для непрерывных величин,
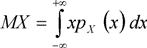(3.4), где рX (х) - плотность вероятности непрерывной случайной величины X. Значение MX характеризует положение центра группирования случайных величин, около которого располагаются, например, размеры большинства деталей в партии.
При отсутствии систематических погрешностей в результатах многократных измерений одной и той же величины в одних и тех же условиях, математическое ожидание можно рассматривать как наибольшее приближение к истинному значению измеряемой величины.
При анализе характера рассеяния размеров деталей, обрабатываемых на станке, математическое ожидание можно рассматривать как размер, на который был настроен станок.
Величину рассеяния значений случайной величины относительно центра группирования определяет параметр, 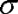который называют средним квадратическим отклонением случайной величины, его определяют по формулам:
для дискретной величины
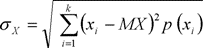(3.5)
для непрерывной величины
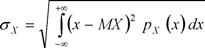(3.6)
Рассеяние случайных величин характеризуется также дисперсией D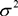X = 
X.
Формула (3.2) выражает уравнение кривой, если начало отсчета расположено на оси x произвольно. При совпадении центра группирования с началом отсчета величины x уравнение кривой нормального распределения будет иметь вид
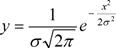(3.7)
В тоже время существуют другие законы распределения, описывающие случайные величины, природа возникновения которых имеет несколько иной характер.
В рассматриваемом случае необходимо упомянуть закон Максвелла, которому подчиняются существенно положительные величины, например: рассеяние значений эксцентриситета, радиальное и торцевое биения, отклонения от соосности, дисбаланс и другие величин, которые не могут принимать отрицательные значения.
Для оценки надёжности работы изделий используют закон Вейбулла, который даёт представление о вероятности отказов.
Получили распространение также закон Симпсона или закон треугольника и закон равной вероятности.
Однако, для обработки результатов наблюдений в основном применяют закон нормального распределения - закон Гаусса.
Вероятность попадания величины в заданный интервал можно определить следующим образом. Ветви теоретической кривой нормального распределения (рис. 3.3) уходят в бесконечность, асимптотически приближаясь к оси абсцисс. Площадь, ограничиваемая кривой и осью абсцисс, равна вероятности того, что случайная величина, например, погрешность размера, лежит в интервале ± 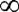. Площадь под кривой распределения равна 1 или 100%, она определяется интегралом
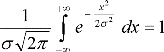(3.8)
Начало координат расположено в точке, совпадающей с центром группирования. Так как подынтегральная функция четная и кривая симметрична относительно максимальной ординаты, можно записать
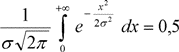(3.9)
Для выражения случайной величины x в долях ее 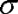примем: x / 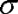= z, откуда x = 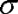z, d x = 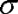d z. В этом случае абсцисса на рис. 3.3 будет выражена в долях 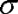. Если принять за пределы интегрирования 0 и z, то интеграл в выражении (3.8) будет функцией z, т.е.
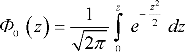(3.10)
Функцию Ф 0 (z) называют нормированной функцией Лапласа: Ф 0 (0) = 0; Ф 0 (- z) = - Ф 0 (z); Ф 0 (- 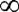) = - 0,5; Ф 0 (+ 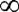) = 0,5.
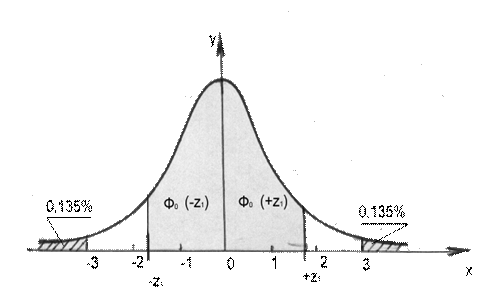
Из формулы (3.9) и рис. 3.4 следует, что площадь, ограниченная отрезком - z 1 + z 1 оси абсцисс, кривой плотности вероятности и двумя ординатами, соответствующими границам отрезка, представляет собой вероятность попадания случайной величины z 1, в данный интервал.
Данные для функции Ф 0 (z) приводятся в справочниках. Пользуясь этими данными можно определить вероятность того, что случайная величина x, выраженная через 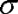, будет находиться в пределах того или иного интервала ± z 1 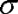. Например, находим, при z 1 = 3, что соответствует случайной величине x = 3 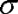, Ф 0 (3) = 0,49865 или Ф 0 (- 3) - Ф 0(3) = 2 Ф 0 (3) = 0,9973.
Так как площадь, ограниченная кривой Гаусса и осью абсцисс, равна 1, то площадь, лежащая за пределами значений х = ± 3 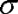, равна 1 - 0,9973 = 0,0027 и расположена симметрично по 0,00135 или по 0,135% справа и слева относительно оси у (см. рис. 3.4).
Следовательно, с вероятностью, близкой к единице, можно утверждать, что случайная величина X не будет выходить за пределы ± 3 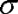. Поэтому при распределении случайной величины по закону Гаусса поле рассеяния, равно V lim = 6 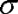или диапазон ± 3 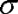считают за практически предельное поле рассеяния случайной величины и принимают за норму точности - допуск. При этом вероятность выхода случайной величины за пределы значений ± 3 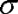равна 0,0027 или 0,27%.
В условиях производства из-за ограниченности числа измерений при обработке вместо математического ожидания и дисперсии получают их приближенные статистические оценки - соответственно эмпирическое среднее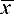 
и эмпирическую дисперсию 
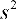, характеризующие средний результат измерений и степень рассеяния результатов. Эти оценки определяют по формулам:
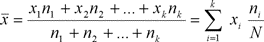(3.11)
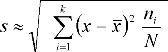(3.12)
В этих выражениях xi - значение, соответствующее середине i -гo интервала, a k - число интервалов. Чем меньше величина s, тем выше точность процесса изготовления или измерения, т. е. тем меньше величины случайных погрешностей. Поэтому параметр s используют в качестве меры точности процесса изготовления или при повторных измерениях одной и той же величины в качестве меры точности метода измерения.
