Обработка результатов измерений статистическими методами применяется на практике для решения следующих задач:
· определение погрешности средств измерений;
· определение соответствия параметров технологического процесса заданной точности изделия;
· установление технологического допуска при обработке;
· определение точностных характеристик установочных и выборочных партий деталей, с целью контроля и управления качеством продукции;
· установление рассеяния показателей качества однотипных изделий и др.
Результаты измерений получаются путём соответствующей обработки результатов наблюдений, показаний полученных с помощью средств измерений.
При этом вводятся следующие понятия:
· результат наблюдения - значение величины отсчёта показаний средства измерений, полученное при отдельном измерении;
· результат измерения - значение величины, полученное после обработки результатов наблюдений.
При изготовлении партии деталей неизбежно происходит рассеяние их геометрических и физико-механических параметров. Поэтому результаты измерения параметров каждой отдельной детали являются случайными величинами. Тоже самое происходит при многократном измерении одной детали с помощью конкретного средства измерений.
При изготовлении и проведении измерений возникают систематические и случайные погрешности.
Систематическими называют погрешности, постоянные по величине и знаку или изменяющиеся по определенному закону в зависимости от действия определённых заранее предсказуемых причин.
Систематические погрешности возникают, например, из-за: неточной настройки оборудования, погрешностей измерительного прибора, отклонения рабочей температуры от нормальной (в т.ч. субъективных действий оператора), силовых деформаций, и др.
Систематические погрешности измерения могут быть полностью или частично устранены, например, при помощи поправочной таблицы к неправильно градуированной шкале прибора или путем определения средней арифметической величины из нескольких отсчетов в противолежащих положениях, например, при измерении шага и половины угла профиля резьбы, коррекции неправильных действий оператора (влияние на температуру дыхания или прикосновения, превышение усилий).
Случайными называют переменные по величине и знаку погрешности, которые возникают при изготовлении или измерении и принимают то или иное числовое значение в зависимости от ряда случайно действующих причин.
Характерным признаком случайных погрешностей является вариация значений, принимаемых ими в повторных опытах.
Эти погрешности вызываются множеством изменяющихся случайным образом факторов таких, как: неточности элементов средства измерения, припуск на обработку, механические свойства материала, сила резания, измерительная сила, различная точность установки деталей на измерительную позицию и другие, причем в общем случае ни один из этих факторов не является доминирующим.
Погрешности изготовления и измерения являются случайными величинами. Примеры случайных величин: размеры деталей при обработке, зазоры в подвижных соединениях, результаты повторных измерений одной и той же величины и т.п.
Случайные погрешности трудно устранить, поэтому их влияние учитывают при назначении допуска на размер или на какой-либо другой параметр.
Появление того или иного числового значения случайной величины в результате измерений рассматривается как случайное событие. То же самое происходит при проведении, каких либо испытаний продукции, например, для установления его показателей качества.
Отношение числа n случаев появления случайной величины или события A к числу N всех произведенных испытаний, при которых это событие могло появиться, называют частостью, или относительной частотой W (А) = n/N.
При достаточно большом числе испытаний N обнаруживается устойчивость значения указанного отношения для большинства случайных событий. Величина W (A) для события А будет колебаться около некоторого постоянного числа, равного единице. Это число, всегда меньшее единицы, называют вероятностью Р (А) появления события А, т. е. Р (А) является мерой объективной возможноcти появления события А.
Вероятность достоверного события равна единице, невозможного события - нулю.
За приближенное значение вероятности Р (А) события А при достаточном числе испытаний можно принимать частость:
P (A)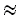 
W (A) = n/N (3.1)
Частость W (A) отличается от вероятности Р (A) тем, что представляет собой случайную величину, которая в различных сериях однотипных испытаний может принимать в зависимости от случайных факторов различные значения, тогда как вероятность Р (А) представляет постоянное для каждого данного события число, определяющее в среднем частость его появления в опытах.
