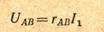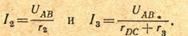Графический метод расчета нелинейной цепи постоянного тока с резистивными элементами

Задача анализа нелинейной цепи. Она состоит в определении токов и напряжений на участках нелинейной цепи при заданных ВАХ НЭ, сопротивлениях линейных элементов и ЭДС (токов) источников.

Вольтамперные ха­рактеристики.

Зависимость напряжения на каком-либо элементе от тока в нем U (/) или зависимость тока от напряжения / ([/) называется вольтамперной характеристикой. Для линейных пассивных элементов вольтамперная характеристика представляет собой прямую, прохо­дящую через начало координат (прямая 1 на рис. 3-1). Для нелинейного элемента она непрямолинейна. Например, вольтамперная характеристика лампы с металлической нитью, имеющей положительный температурный коэффи­циент, отличается от прямой, отклоняясь вниз (кривая 2 на рис. 3-1), а у лампы с угольной нитью, имеющей отри­цательный коэффициент сопротивления, наоборот, отклоняется от прямой вверх (кривая 3 на рис. 3-1).

Расчет нелинейной цепи при последовательном соединении пассивных НЭ. Возможны два метода решения задачи. Первый метод сводится к графическому решению уравнения, составленного по второму закону Кирхгофа.

Для двух последовательно соединенных НЭ1 и НЭ2 (рис. 6.13)

U = U₁ + U₂ (6.1)

где U — общее напряжение на элементах; U₁ и U₂ — на­пряжения на соответствующих элементах.

Для решения задачи ВАХ НЭ строятся в общей системе координат (рис. 6.14). При последовательном соединении в НЭ один и тот же ток, поэтому задаемся несколькими (5—6) значениями тока: I₁, I₂, I₃и т.д., проводим на гра­фике линии, параллельные оси абсцисс, суммируем соот­ветствующие значения напряжений на НЭ1 и НЭ2 и нахо­дим общее напряжение при каждом токе (точки 1, 2, 3...). Соединяя плавной кривой полученные точки, строим ВАХ последовательного соединения, на которой по заданному напряжению U₀ находим искомый ток I₀, а по ВАХ отдель­ных НЭ —напряжения U₁₀и U₂₀на этих НЭ.

Второй метод, называемый методом пересечения харак­теристик, состоит в следующем графическом построении. Для одного из НЭ, например НЭ1, строится (рис. 6.15) его ВАХ I(U₁), аналогичная показанной па рис. 6.14. Напря­жение на НЭ1 определяется еще уравнением U₁ = U₀—U₂, поэтому построим зависимость I= f (U₀ – U₂). ВАХ I(U₂) задана (рис. 6.14). Чтобы получить требуемую зависимость, нужно симметричную относительно оси ординат (зеркальную) характеристику I(—U₂) сместить по оси абсцисс на +U₀. Режим цепи определяет точка пересече­ния N зависимости I (U₀—U ₂) с ВАХ I(Ui), так как ток в обоих НЭ один и тот же.

 

 

 

Метод пересечения характеристик относительно часто применяется в различного рода задачах, так как не требу­ет графического построения результирующей характеристи­ки. Он особенно удобен, когда одно из сопротивлений нели­нейное, а другое — линейное и его ВАХ — прямая.

Расчет нелинейной цепи при параллельном соеди­нении НЭ (рис. 6.18). При параллельном соединении НЭ

I = I₁ + I₂

ВАХ элементов должны быть заданы и построены в общей системе координат (рис. 6.19). Для построения ВАХ параллельного соединения задаемся несколькими значе­ниями напряжений U₁, U₂, U₃... и т. д. и согласно (6.2),
суммируя соответствующие значения токов, получаем точки суммарной ВАХ. Соединяя плавной кривой полученные точки /, 2, 3..., строим ВАХ цепи.

 

Расчет нелинейной цепи при смешанном соедине­нии НЭ. Расчет сводится к двум предыдущим случаям.

Порядок расчета рассмотрим на примере.

Пример 6.2. Стабилизатор напряжения (рис. 6.20) выполнен на ста­билитроне ист. ВАХ которого изображена на рис. 6.21 (кривая 1). Стабилитрон включен параллельно сопротивлению нагрузки, напряже­ние на котором требуется стабилизировать; R — сопротивление резистора для гашения части напряжения. Определить границы изменения на­пряжения питания U, при которых на сопротивлении нагрузки поддер­живается почти постоянное напряженно, близкое к 150 В.

Решение. Проводим ВАХ сопротивления нагрузки R_K (с учетом масштабов) — кривая 2; строим ВАХ параллельного разветвления Ra и Re, суммируя токи при фиксированных значениях напряжения— кривая 3; резистора R (с учетом масштабов) —кривая 4; цепи, состоя* щей из последовательного соединения резистора R и параллельного со­единения Rt и Rcr — кривая 5.

2.ЦЕПИ С ОДНИМ ИСТОЧНИКОМ ПИТАНИЯ И СМЕШАННЫМ СОЕДИНЕНИЕМ СОПРОТИВЛЕНИЙ

Смешанным соединением сопротивлений называют сочетание их последовательных и параллельных соединений. Наиболее простым и распространенным в практике смешанным соединением является цепь обычного параллельного подключения потребителей к распре­делительному щитку при подсоединении этого щитка к источнику питания с помощью проводов.

Пусть все сопротивления и напряжение на входе этой схемы заданы и требуется определить токи ее отдельных участков. Для расчета воспользуемся методом эквивалентных со­противлений, по которому отдельные участки схемы упро­щают и постепенным преобразованием их приводят схему к одному общему (входному) сопротивлению. Для упрощения схемы отдель­ные группы последовательно или параллельно соединенных сопро­тивлений заменяют одним эквивалентным сопротивлением.

Так, сопротивления r_t и г_ь схемы рис. 2.6, а соединены парал­лельно и их можно заменить одним эквивалентным сопротивлением

После этого схема несколько упрощается (б).

Сопротивление г_ав включено последовательно с сопротивлением r₁, как указано на схеме рис. 2. 6, в. Общее, или входное, сопротивле­ние этой схемы г_вх = г_ав + r ₁ дает возможность определить общий ток I₁