Построение эпюр M И Q в шарнирной балке
Постановка задачи и анализ расчетной схемы балки
В учебном пособии [3] приведен пример построения указанных эпюр аналитическим способом для шарнирной балки, изображенной на рис. 3.1,а.
Расчет был выполнен для варианта, когда
Выполним построение этих эпюр с помощью ПВК SCAD при l = 6 м и q =10 кН/м.
Перед началом работы на компьютере необходимо выполнить две подготовительных операции с заданной расчетной схемы балки:
1) Проверить является балка статически определимой или статически неопределимой системой. Это связано с тем, что для статически определимых систем при определении в них только усилий упрощается задание жесткостей стержней при использовании программы SCAD (см. подраздел 1.6).
2) Вручную разбить балку на конечные элементы типа 2 (стержневой элемент плоской рамы, см. рис.1.3) с учетом особенностей ее конструкции и вида, действующей на нее нагрузки. действующей на нее нагрузки.
При этом выбрать начало координат общей системы осей координат и продумать вопрос о методике построения расчетной схемы для МКЭ с помощью программы SCAD (см. подразделы 1.4 ¸1.6 раздела 1 учебного пособия).
Первая операция состоит из двух пунктов:
а) Сначала подсчитываем степень статической неопределимости n балки. Для этого используем формулу [3÷5]:
 ,
| (3.1) |
где n оп ─ число неизвестных составляющих опорных реакций во всех опорах балки;
n ш1─ число уравнений равновесия вида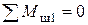 
, которые можно записать для каждого одиночного шарнира дополнительно к имеющимся трем уравнениям равновесия для всей балки.
В рассматриваемой балке n оп = 5; n ш1 = 2. В результате по указанной формуле получаем необходимое условие статической определимости балки: n = 0.
б) Затем исследуем геометрическую неизменяемость рамы. В данном случае для этого достаточно использовать структурный анализ балки.
Действительно (Рис.3.1,б), заданную балку можно рассматривать как систему, состоящую из трех жестких дисков (ABE, ECF и FD). Диск ABE неподвижно прикреплен к основанию тремя опорными связями и, таким образом, геометрически неизменяем. Диск ECF прикреплен двумя связями к неподвижному диску ABE и одной связью с неподвижным основанием, поэтому он также геометрически неизменяем. Аналогично доказывается, что диск FD геометрически неизменяем, а значит, геометрически неизменяема и вся заданная шарнирная балка.
Таким образом, на основании исследований, выполненных в пунктах а) и б), делаем вывод о том, что заданная балка является статически определимой системой.
Второй подготовительной операцией является подготовка к формированию расчетной схемы МКЭ заданной балки с помощью программы SCAD:
1) Еще раз изображаем заданную расчетную схему балки (Рис.3.1,в);
2) С учетом нагрузки (см. указания в подразделе 1.7), разбиваем стержни на элементы и нумеруем узлы и элементы (см. рис.3.1,в).
3) Нумерацию узлов выполняем с учетом рекомендаций подразделов 1.3, 1.4 и 1.7.
4) Выбираем начало общей системы осей координат (узел 1 на рис.3.1,в);
5) Рядом с номером узла указываем его координату X в общей системе координат X, Y, Z (так как балка представляет собой элементы, лежащие на оси X, координаты Y и Z у всех узлов равны нулю и на рис.3.1, в не указываются).
