Рассмотрим систему состоящую из информационных средств и средств управления производством. Информационная система обладая определёнными техническими средствами обнаруживает … определённые проявления фактов.
Пусть ИС имеет различные средства, которые позволяет ей обнаруживать ν 
фактов в единицу времени. Естественно предположить что промежутки времени между моментами обнаружения фактов являются величинами случайными. Обнаруженные факты во времени образуют поток который весьма близкий к потоку Пуассона. Данные информационной системы об обнаруженных признаках поступают в систему обработки данных и управления силами и средствами (ресурсами), которая имеет ограниченную пропускную способность по обработке полученной информации в единицу времени.
Обозначим пропускную способность системы управления через 
.
Время обработки данных о требуемом признаке является величиной случайной. Обработанные в системе данные о признаках распределяются далее между выделенными силами и средствами, решающих соответствующие целевые задачи.
Рассмотрим случай, когда время пребывания требуемых признаков (фактов) в области действия информационно-управляющей системы весьма ограниченно и соизмеримо со временем, которое необходимо для их идентификации, обработки исходных данных и адекватных действий по этим признакам. Поэтому эту сложную систему можно в первом приближении рассматривать как систему с отказами.
Обозначим вероятности состояний системы:
Р 
- информационная система и система управления свободны от обслуживания признаков и не проявляют себя.
Р 
- информационная система занята получением информации по об одном признаке, система управления свободна от обслуживания.
Р 
- информационная система свободна, а система управления занята обработкой информации о признаке и выработкой решения на применение сил и средств.
Р 
- обе системы заняты.
Составим дифференциальные уравнения состояний информационно-управляющей системы. Обозначим соответственно состояния системы А , А , А , А .
Состояние А возможно в следующих несовместных случаях:
-в момент времени t информационная система и система управления свободны. За интервал времени Δt в области действия СУ не проявился ни один признак. Вероятность этого события равна
Р (t) (1 - λ Δt); (3.1.)
- в момент времени t ИУС находилась в состоянии А . За время Δt данные о требуемом признаке переданы силам и средствам воздействия. Вероятность этого события равна
Р (t) Δt; (3.2.)
Тогда соотношение для состояния А запишется в следующем виде
Р (t+Δt)=Р (t)(1-λΔt)+ Р (t) Δt) ν 
Δt (3.3.)
После соответствующих преобразований и перехода к пределу при Δt→ 0, получим
Р (t) = - Р (t) λ + Р (t)ν . (3.4.)
Рассмотрим состояние ИУС А . Оно возможно в следующих несовместных случаях:
- ИУС в момент времени t находится в состоянии А . За интервал времени Δt в области действия ИУС не проявился ни один новый факт и не было осуществлено обслуживание поставок соответствующими силами и средствами.
Вероятность этого события равна
Р (t) (1 - λ Δt)(1- ν Δt); (3.5.)
- в момент времени t ИУС находилась в состоянии А . За время Δt ИС обнаружила и выдала данные о требуемом факторе СУ,
Р (t) (ν Δt); (3.6.)
- в момент времени t ИУС находилась в состоянии А . За время Δt ИС обнаружила и выдала данные о требуемом факторе СУ, но СУ не использовала их, так как была занята обработкой данных по предыдущему факту. И поэтому полученные данные были безвозвратно потеряны вследствие кратковременности пребывания фактора в области действия ИУС.
Вероятность этого события равна
Р (t) ν Δt. (3.7.)
Тогда соотношение для состояния А запишется в следующем виде
Р (t) = - Р (t)(λ+ ν ) + Р (t) ν + Р (t) ν . (3.7.)
При составлении дифференциального уравнения состояние ИУС А необходимо исходить из того, что оно возможно в следующих несовместных случаях:
- в момент времени t ИУС находилась в состоянии А . За интервал времени Δt в области действия ИУС проявился требуемый фактор и он был идентифицирован ИС. Вероятность этого события равна
Р (t) λ Δt; (3.8.)
- в момент времени t ИУС находилась в состоянии А . За время Δt в области действия ИУС проявился требуемый фактор и он не был идентифицирован ИС и данные не были переданы в СУ. Вероятность этого события равна
Р (t)(1- ν Δt); (3.9.)
- в момент времени t ИУС находилась в состоянии А .За время Δt СУ СУ выдала данные для воздействия соответствующих Сил и Средств на соответствующий фактор. Вероятность этого события равна
Р (t) ν Δt. (3.10.)
Тогда соотношение для состояния А запишется в следующем виде
Р (t) = Р (t) λ - Р (t)ν + Р (t)ν . (3.11.)
Наконец, последнее состояние ИУС А возможно в следующих несовместных случаях:
- в момент времени t ИУС находилась в состоянии А . За время Δt получены новые данные о требуемых признаках
Р (t) λ Δt; (3.12.)
--в момент времени t ИУС была в состоянии А . За интервал времени Δt не были обработаны данные по требуемым признакам ИС и СУ в область действия З П С проявилась новые поставки. Вероятность этого события равна
Р (t)(1- (ν + ν )Δt); (3.13.)
Тогда соотношение для состояния А запишется в следующем виде
Р (t) = Р (t))λ+ Р (t)(ν + ν ). (3. 14.)
Общая система уравнений, описывающая все возможные состояния ИУС, представляется в следующем виде из четырёх ДУ:
Р (t) = - Р (t) λ + Р (t)ν .
Р (t) = - Р (t)(λ+ ν ) + Р (t) ν + Р (t) ν . (3.15.)
Р (t) = Р (t) λ - Р (t)ν + Р (t)ν .
Р (t) = Р (t))λ+ Р (t)(ν + ν ).
При стационарном решении, т.е. при допущении, что переходные процессы отсутствуют,
Для стационарных процессов мы предполагаем, что переходные процессы в системе отсутствуют. Это позволяет сделать следующую запись свойств для вероятностей перехода:
t → ∞, Р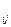 
(t) →0, Р 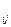(t) =Р 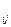= const. Тогда дифференциальные уравнения преобразуются в алгебраические:
Р (t) λ = Р (t)ν .
Р (t)(λ+ ν )= Р (t) ν + Р (t) ν . (3.16.)
Р (t)ν =Р (t) λ + Р (t)ν .
Р (t)(ν + ν ) = Р (t))λ.
Решая систему алгебраических уравнений (3.16), можно определить вероятности различных состояний информационно-управляющей системы:
Р = 
Р = 
Р = 
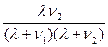
Р = = 
Где λ – интенсивность проявления очередных признаков потенциально-опасного процесса в зоне ответственности ИУС.
Вероятность того, что цель останется не идентифицированной и не обслуженной и выполнит свою задачу равна
Р 
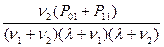=1- 
=1-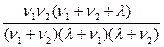 
.
Пример. Пусть в области ответственности ИУС требуемый признак появляется 2 раза в единицу времени (λ= 2 пр./ед. вр.). Информацтионная система обладает такими средствами, что которые позволяют ей в заданном районе при сложившейся обстановке в среднем обнаруживать в единицу времени два признака (ν = 2 пр./ед. вр.). Система управления может обработать спланировать обслуживание в среднем по 4 признака в единицу времени ν = 4пр./ед. вр.).
Определим вероятность не обслуживания каждого признака.
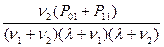Р =1- =1- 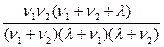.= 0,44. УТВЕРЖДЕНА
постановлением Правительства
Российской Федерации
от 17 октября 2006 г. № 613
