Функция с фиксированными пропорциями факторов (функция Леонтьєва).
, (5.1)
где а 1, а 2 — параметри.
Известно несколько альтернативных систем (гипотез), которые виокремлюють функции этого вида:
а) предельная производительность первого фактора есть двухуровневой кусков-постоянной невозрастающей функцией от соотношения с нулевым нижним уровнем. Предельная производительность второго фактора - ненисходящая кусков-постоянная функция от с нулевым нижним уровнем;
б) функция есть розв'язком такой задачи математического программирования:
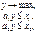
де у — сменная, которую оптимізують;
в) функция есть однородной, а эластичность замены факторов равняется нулю;
г) функция может быть получена из функции с постоянной эластичностью вида
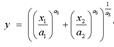
путем предельного перехода: 
Функция Леонтьєва предназначена в основном для моделирования строго детермінованих технологий, которые не допускают отклонения от технологических норм и нормативов относительно использования ресурсов на единицу продукции. Как правило, она используется для формализованного описания мелкомасштабных или целиком автоматизированных объектов.
Функция Кобба-Дугласа
. (5.2)
Здесь также используется несколько систем гипотез, которые виокремлюють класс функций Кобба-Дугласа среди дважды дифференцированных функций от двух сменных:
а) эластичности выпуска за факторами есть постоянными:
.
Розв'язок этой системы дифференционных уравнений в частинних производных первого порядка належит к классу функций Кобба-Дугласа;
б) эластичность функции за одним из факторов есть постоянной, и функция есть однородной;
в) функция есть однородной, а эластичности уменьшения факторов за Алленом и Михайловським равняются единицы;
г) предельная производительность каждого фактора есть пропорциональной его средней производительности;
д) функция есть однородной как функция от х 1, х 2 и как функция от х 1 за любого фиксированного х 2;
е) функция может быть получена из функции с постоянной эластичностью путем осуществления замены вида
и предельного перехода а 3 ® 0. Функция Кобба-Дугласа наиболее частое используется для формализованного описания середньомасштабних хозяйственных объектов и экономики страны.
Линейная функція
. (5.3)
Предпосылки и гипотезы:
а) предельные производительност факторов есть постоянными:
,
а в нуле функция приобретает нулевого значения;
б) предельная производительность одного из факторов есть постоянной, и функция однородная первой степени:
;
в) функция однородная, и эластичность замены факторов, за Алленом, есть бесконечной;
г) эластичность выпуска за факторами обратно пропорциональная их средний производительности.
Линейная функция применяется для моделирования крупномасштабных систем (большая область, народное хозяйство в целом), в которых выпуск продукции есть результатом одновременного функционирования большого количества разнообразных технологий. Особую роль сыграет гипотеза постоянности предельных производственных факторов ли их неограниченного замещения.
9. ВОПРОС 9. Экономико-математическая модель межотраслевого баланса (модель Леонтьева «затраты-выпуск»).
Основу информационного обеспечения модели межотраслевого баланса составляет технологическая матрица, которая содержит коэффициенты прямых материальных затрат на производство единицы продукции. Эта матрица есть базой экономико-математической модели межотраслевого баланса.
Допускает гипотеза, в соответствии с которой для производства единицы продукции в j -й области необходимое определенное количество затрат промежуточной продукции і- ї области, которые составляет aij, и эта величина не зависит от объемов производства в j -й области и есть довольно стабильной величиной в времени. Величины aij называют коэффициентами прямых материальных затрат и вычисляют таким образом:
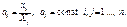(11.4)
Коэффициенты прямых материальных затрат показывают, какое количество продукции і- ї галузі необходимо израсходовать, если учитывать лишь прямые затраты, для производства единицы продукции j- ї области. С учетом формулы (11.4) систему уравнений баланса (11.2) можно записать в виде
Хі 
Хі 
(11.5)
Если ввести к рассмотрению матрицу коэффициентов прямых материальных затрат А = (аij), вектор-столбик валовой продукции X и вектор-столбик конечной продукции Y:
это система уравнений (11.5) в матричной форме будет иметь вид
X = AX + Y. (11.6)
· Систему уравнений (11.5), в ли матричной форме (11.6), называют экономико-математической моделью межотраслевого баланса (моделью Леонтьєва, моделью "затраты - выпуск"). С помощью этой модели можно выполнить три варианта вычислений:
· " задавая в модели объемы валовой продукции каждой области (Хi), можно определить объемы конечной продукции каждой области(Yi):
Y = (E – A) X, (11.7)
где Е — единичная матрица n-го порядка;
· " задавая объемы конечной продукции всех областей (Yi), можно определить объемы валовой продукции каждой области (Хi):
X = (E – A)–1 Y; (11.8)
" для ряда областей задавая объемы валовой продукции, а для остатка - объемы конечной продукции, можно отыскать величины конечной и валовой продукции всех областей.
В формулах (11.7) и (11.8) Е обозначает единичную матрицу
n-го порядка, а (Е – А)–1 — матрицу, обратную к матрице (Е – А).
