8.2.1 Расчет на прочность балок 1-го класса следует выполнять по формулам: при действии момента в одной из главных плоскостей
 (41)
(41)
при действии в сечении поперечной силы
 (42)
(42)
при действии моментов в двух главных плоскостях (и наличии бимомента)
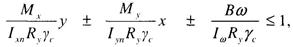 (43)
(43)
где х и у - расстояния от главных осей до рассматриваемой точки сечения;
при одновременном действии в стенке балки момента и поперечной силы
 (44)
(44)
где σх = Мх у / Iхп - нормальное напряжение в срединной плоскости стенки, параллельное продольной оси балки;
σy - то же, перпендикулярное продольной оси балки, в том числе σloc, определяемое по формуле (47);
τ xy = QS/ (Itw) -касательное напряжение в стенке.
Напряжения σх и σy, принимаемые в формуле (44) со своими знаками, а также τ xy, следует определять в одной и той же точке стенки балки.
В балках, рассчитываемых по формуле (43), значения напряжений в стенке балки должны быть проверены по формуле (44) в двух главных плоскостях изгиба.
При ослаблении стенки отверстиями для болтов левую часть формулы (42), а также значение τ xy, в формуле (44) следует умножать на коэффициент α, определяемый по формуле
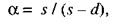 (45)
(45)
где s - шаг отверстий в одном ряду;
d - диаметр отверстия.
8.2.2 Расчет на прочность стенки балки, не укрепленной ребрами жесткости, при действии местного напряжения σloc в местах приложения нагрузки к верхнему поясу, а также в опорных сечениях балки следует выполнять по формуле
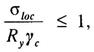 (46)
(46)
где
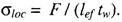 (47)
(47)
Здесь F - расчетное значение нагрузки (силы);
lef - условная длина распределения нагрузки, определяемая по формулам: для случаев по рисунку 6, а и б
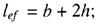 (48)
(48)
для случая по рисунку 6, в
 (49)
(49)

а - сварная; б - прокатная; в - сварная или прокатная при нагрузке от колеса крана
Рисунок 6 - Схемы распределения сосредоточенной нагрузки на стенку балки
где h - размер, равный сумме толщины верхнего пояса балки и катета поясного шва, если нижняя балка сварная (см. рисунок 6, а), либо расстоянию от наружной грани полки до начала внутреннего закругления стенки, если нижняя балка прокатная (см. рисунок 6, б);
ψ - коэффициент, принимаемый равным: 3,25 - для сварных и прокатных балок; 4,5 - для балок с фрикционными поясными соединениями;
I 1 f - сумма собственных моментов инерции пояса балки и кранового рельса или момент инерции сечения, состоящего из пояса и рельса в случае приварки рельса швами, обеспечивающими совместную работу пояса и рельса.
8.2.3 Расчет на прочность разрезных балок 2-го и 3-го классов двутаврового и коробчатого сечений (рисунок 7) из стали с нормативным сопротивлением Ryn ≤ 440 Н/мм2 при соблюдении требований 8.4.6, 8.5.8, 8.5.9 и 8.5.18 и при касательных напряжениях τх = Qx/Aw ≤ 0,9 Rs (кроме опорных сечений) следует выполнять по формулам:
при изгибе в плоскости наибольшей жесткости (Ix > I y)
 (50)
(50)
при изгибе в двух главных плоскостях и напряжениях τy = Qx/ (2 Af) ≤ 0,5 Rs
 (51)
(51)
Здесь Мх, My - абсолютные значения изгибающих моментов;
сх, су - коэффициенты, принимаемые согласно таблице Е.1;
β - коэффициент, принимаемый равным:
при τx ≤ 0,5 Rs β = 1;
при 0,5 Rs < τx ≤ 0,9 Rs
 (52)
(52)
где α f = Af / Aw - отношение площади сечения пояса к площади сечения стенки (для несимметричного сечения Af - площадь меньшего пояса;
для коробчатого сечения Aw - суммарная площадь сечений двух стенок).

Рисунок 7 - Схемы двутаврового (а) и коробчатого (б) сечений балок с действующими на них усилиями
При расчете сечения в зоне чистого изгиба в формулах (50) и (51) следует принимать β = 1 и вместо коэффициентов сх и су соответственно
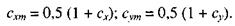 (53)
(53)
Расчет на прочность в опорном сечении балок (при Мх = 0 и Му = 0) следует выполнять по формулам:
 (54)
(54)
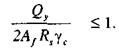 (55)
(55)
При ослаблении стенки отверстиями для болтов левую часть формул (54) и (55) следует умножать на коэффициент а, определяемый по формуле (45).
С целью установления размеров минимальных сечений составных балок значения коэффициентов сх и су допускается принимать меньше значений, приведенных в таблице Е.1, но не менее 1,0. Методика подбора минимальных сечений изгибаемых элементов приведена в приложении М.
8.2.4 Расчет на прочность разрезных балок переменного сечения согласно 8.2.3 с учетом пластических деформаций допускается выполнять только в одном сечении с наиболее неблагоприятным сочетанием усилий М и Q; в остальных сечениях балки расчет следует выполнять при значениях коэффициентов сх и су меньших, чем в таблице Е.1 приложения Е, или согласно 8.2.1.
8.2.5 Расчет на прочность неразрезных и защемленных балок постоянного двутаврового и коробчатого сечений с двумя осями симметрии, изгибаемых в плоскости наибольшей жесткости, со смежными пролетами, отличающимися не более чем на 20 %, при соблюдении требований 8.4.6, 8.5.8, 8.5.9 и 8.5.18 следует выполнять по формуле (50) как сечений 2-го класса с учетом частичного перераспределения опорных и пролетных моментов.
В этом случае расчетное значение момента следует определять по формуле
 (56)
(56)
где М mах - наибольший изгибающий момент в пролете или на опоре, определяемый из расчета неразрезной балки в предположении упругой работы стали;
Mef - условный изгибающий момент, равный:
а) в неразрезных балках с шарнирно опертыми концами большему из значений:
 (57)
(57)
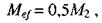 (58)
(58)
где символ max означает, что следует найти максимум всего следующего за ним выражения;
М 1 - изгибающий момент в крайнем пролете, вычисленный как в свободно опертой однопролетной балке;
а - расстояние от сечения, в котором действует момент М 1, до крайней опоры;
l - длина крайнего пролета;
М 2 - максимальный изгибающий момент в промежуточном пролете, вычисленный как в шарнирно опертой однопролетной балке;
б) в однопролетных и неразрезных балках с защемленными концами Mef = 0,5 M 3, где М3 - наибольший из моментов, вычисленных как в балках с шарнирами на опорах;
в) в балке с одним защемленным и другим свободно опертым концом значение Mef следует определять по формуле (57).
Значение τх в формуле (52) следует вычислять в сечении, где действует М mах; если М mах - момент в пролете, следует проверить опорное сечение балки.
8.2.6 Расчет на прочность неразрезных и защемленных балок, удовлетворяющих 8.2.5, в случае изгиба в двух главных плоскостях следует выполнять по формуле (51) с учетом перераспределения опорных и пролетных моментов в двух главных плоскостях согласно указаниям 8.2.5.
8.2.7 Расчет на прочность неразрезных и защемленных балок, удовлетворяющих требованиям 8.2.5, 8.4.6, 8.5.8, 8.5.9 и 8.5.18, допускается выполнять по формуле (50) как сечений 3-го класса с учетом перераспределения изгибающих моментов и образования условных пластических шарниров, а также влияния касательных напряжений τх в соответствии с 8.2.3 в сечениях с максимальным изгибающим моментом.
8.2.8 Расчет на прочность бистальных разрезных балок двутаврового и коробчатого сечений с двумя осями симметрии при соблюдении требований 8.4.4, 8.5.9 и 8.5.17 и при касательных напряжениях τх ≤ 0,9 Rs и τy ≤ 0,5 Rs (кроме опорных сечений) следует выполнять как расчет сечений 2-го класса по формулам:
при изгибе в одной главной плоскости
 (59)
(59)
при изгибе в двух главных плоскостях
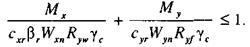 (60)
(60)
В формулах (59) и (60) обозначено:
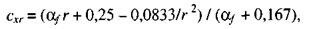 (61)
(61)
где α f = Af/Aw; r = Ryf / Ryw;
β r - коэффициент, принимаемый равным:
при τх ≤ 0,5 R s β r = l;
при 0,5 Rs < τх < 0,9 Rs
 (62)
(62)
cyr - коэффициент, принимаемый равным 1,15 - для двутаврового сечения и 1,05/ r - для коробчатого сечения.
Расчет бистальных балок при наличии зоны чистого изгиба и в опорном сечении, а также с учетом ослабления сечения следует выполнять согласно 8.2.3 и приложению М.






