Фотоэффект.
 |

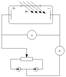 Под фотоэффектом понимают изменение состояния электронов в веществе под действием света (эл.маг излучения). Различают внутренний и на внешний фотоэффекты. При внутреннем фотоэффекте электроны с поверхности вещества не вырываются. Внешний фотоэффект состоит в вырывании электронов с поверхности вещества под действием электромагнитного излучения Сущность внешнего фотоэффекта: Сквозь кварцевую пластинку на катод подал свет. При этом, при отсутствии внешнего напряжения, амперметр показывал некоторый небольшой ток. При включении внешнего напряжения, ток в цепи возрастал почти линейно до некоторого значения. После этого наступал эффект насыщения. В то же время, при нулевом напряжении, некоторый ток существовал. Прикладывая отрицательное напряжение, получим нулевой ток. Величина фототока зависит как от длины падающей волны, так и от интенсивности излучения. Вообще говоря, интенсивностью излучения называют энергию, проходящую за единицу времени через поверхность единичной площади. Зависимость напряжения от различной частоты падающего излучения, показана на рисунке 3а. Здесь ν3< ν1< ν2, то есть с увеличением частоты, режим насыщения наступает при большем токе до какого-то определённого уровня. Потом дальнейший рост частоты уже не приводит к росту тока, а, наоборот, к его уменьшению. Качественно это показано на рисунке 3в. Зависимость фототока от интенсивности излучения приведена на рисунке 3б.
Под фотоэффектом понимают изменение состояния электронов в веществе под действием света (эл.маг излучения). Различают внутренний и на внешний фотоэффекты. При внутреннем фотоэффекте электроны с поверхности вещества не вырываются. Внешний фотоэффект состоит в вырывании электронов с поверхности вещества под действием электромагнитного излучения Сущность внешнего фотоэффекта: Сквозь кварцевую пластинку на катод подал свет. При этом, при отсутствии внешнего напряжения, амперметр показывал некоторый небольшой ток. При включении внешнего напряжения, ток в цепи возрастал почти линейно до некоторого значения. После этого наступал эффект насыщения. В то же время, при нулевом напряжении, некоторый ток существовал. Прикладывая отрицательное напряжение, получим нулевой ток. Величина фототока зависит как от длины падающей волны, так и от интенсивности излучения. Вообще говоря, интенсивностью излучения называют энергию, проходящую за единицу времени через поверхность единичной площади. Зависимость напряжения от различной частоты падающего излучения, показана на рисунке 3а. Здесь ν3< ν1< ν2, то есть с увеличением частоты, режим насыщения наступает при большем токе до какого-то определённого уровня. Потом дальнейший рост частоты уже не приводит к росту тока, а, наоборот, к его уменьшению. Качественно это показано на рисунке 3в. Зависимость фототока от интенсивности излучения приведена на рисунке 3б.
Рассмотрим его законы. Законы фотоэффекта.
1. Закон Столетова. Существует граничная частота 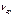 , ниже которой для данного материала катода фотоэффект отсутствует независимо от плотности светового потока энергии и продолжительности облучения катода. Эта граничная частота называется красной границей Значение этой границы зависит только от рода атомов. Энергия, которую нужно затратить, чтобы вырвать электрон из вещества, называется работой выхода.
, ниже которой для данного материала катода фотоэффект отсутствует независимо от плотности светового потока энергии и продолжительности облучения катода. Эта граничная частота называется красной границей Значение этой границы зависит только от рода атомов. Энергия, которую нужно затратить, чтобы вырвать электрон из вещества, называется работой выхода.  .
.
2. Закон фотоэффекта. Максимальная энергия фотоэлектрона, покидающего катод, равна  ; не зависит от плотности энергии светового потока и линейно зависит от частоты.
; не зависит от плотности энергии светового потока и линейно зависит от частоты.
3. Закон фотоэффекта. При фиксированной частоте излучения число электронов, выбиваемых из катода в единицу времени, прямо пропорционально плотности светового потока энергии.
Обобщая законы фотоэффекта, Эйнштейн записал уравнение фотоэффекта: 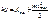 - энергия фотона, попадающего на катод, идёт на преодоление работы выхода электрона из материала катода и на сообщение ему кинетической энергии.
- энергия фотона, попадающего на катод, идёт на преодоление работы выхода электрона из материала катода и на сообщение ему кинетической энергии.
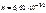 Дж·с.
Дж·с.
Возвращаясь к различным видам фотоэффекта, необходимо заметить, что существует так называемый ядерный фотоэффект. Так называют явление поглощения сильно коротковолнового излучения (рентгеновского или  – излучения) ядрами атомов, в результате которого происходит вылет нуклонов (протонов и нейтронов) из ядер.
– излучения) ядрами атомов, в результате которого происходит вылет нуклонов (протонов и нейтронов) из ядер.
2. Эффект Комптона.
Исследуя спектр, Комптон заметил, что лучи, рассеянные на угол меньше  , обладают большей длиной волны, чем исходное излучение, так что частота
, обладают большей длиной волны, чем исходное излучение, так что частота  вторичной волны оказывается вопреки классической теории меньше, чем частота
вторичной волны оказывается вопреки классической теории меньше, чем частота  первоначального электромагнитного поля. Причём, энергия рассеянных фотонов (а значит и их частота) зависит от угла рассеяния
первоначального электромагнитного поля. Причём, энергия рассеянных фотонов (а значит и их частота) зависит от угла рассеяния  . Комптон сделал вывод, что сдвиг длины волны
. Комптон сделал вывод, что сдвиг длины волны  линейно пропорционален
линейно пропорционален  , где
, где  – угол рассеяния. Таким образом, чтобы поставить знак равенства, необходимо умножить
– угол рассеяния. Таким образом, чтобы поставить знак равенства, необходимо умножить  на некоторую константу. Мы можем записать:
на некоторую константу. Мы можем записать: 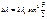 (1), где
(1), где  – комптоновская постоянная (комптоновская длина волны). Рассмотрим теперь графики зависимости
– комптоновская постоянная (комптоновская длина волны). Рассмотрим теперь графики зависимости  для различных
для различных  . Из графиков видно, что функция
. Из графиков видно, что функция  при различных
при различных  имеет максимум не только при исходной длине волны, но и при некоторых других.
имеет максимум не только при исходной длине волны, но и при некоторых других.
Для объяснения эффекта Комптона, Дебай рассмотрел упругое столкновение двух частиц: светового кванта и электрона.
 Пусть до взаимодействия электрон неподвижен. Фотон с импульсом
Пусть до взаимодействия электрон неподвижен. Фотон с импульсом  взаимодействует с электроном мишени, рассеивается на нём. Импульс фотона изменяется и становится равным
взаимодействует с электроном мишени, рассеивается на нём. Импульс фотона изменяется и становится равным 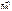 . Электрон также рассеивается и при этом получает импульс
. Электрон также рассеивается и при этом получает импульс 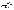 . Таким образом, мы можем записать законы сохранения импульса и энергии:
. Таким образом, мы можем записать законы сохранения импульса и энергии:

В формуле (3) под  подразумевается масса покоя электрона. Проведём некоторые преобразования. Сложим импульс по правилу параллелограмма. Для треугольника
подразумевается масса покоя электрона. Проведём некоторые преобразования. Сложим импульс по правилу параллелограмма. Для треугольника  применим теорему косинусов:
применим теорему косинусов:
 . Так как
. Так как 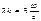 , то
, то
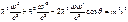 (4).
(4).
 Из равенства (3) следует, что
Из равенства (3) следует, что 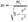 или
или  . Из последнего выражения найдём
. Из последнего выражения найдём  :
: 
 . Подставим последнее выражение в формулу (4), и, учитывая закон сохранения энергии:
. Подставим последнее выражение в формулу (4), и, учитывая закон сохранения энергии:  (получается из формулы (3)), запишем:
(получается из формулы (3)), запишем:
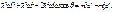


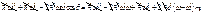
 . Разделим последнее выражение на
. Разделим последнее выражение на  :;
:;  . Так как
. Так как  , то
, то 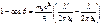 . Преобразуя последнее выражение, получим:
. Преобразуя последнее выражение, получим:  . Обозначим
. Обозначим 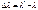 . Тогда
. Тогда 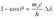 . Отсюда
. Отсюда  или
или  (5). В последней формуле выражение
(5). В последней формуле выражение  является постоянной, так как из таковых состоит. Вычисления показывают, что
является постоянной, так как из таковых состоит. Вычисления показывают, что  , что в точности совпадает с комптоновской постоянной. Таким образом, (5) можно переписать так
, что в точности совпадает с комптоновской постоянной. Таким образом, (5) можно переписать так 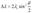 , что в точности совпадает с опытной формулой (1). Из полученного соотношения следует, что квантовая теория хорошо объясняет эффект Комптона, исходя из корпускулярных свойств излучения.
, что в точности совпадает с опытной формулой (1). Из полученного соотношения следует, что квантовая теория хорошо объясняет эффект Комптона, исходя из корпускулярных свойств излучения.
Интерференция фотонов.
 Из курса электричества известно, что к электромагнитной волне может быть применено скалярное волновое уравнение:
Из курса электричества известно, что к электромагнитной волне может быть применено скалярное волновое уравнение:  (1), где
(1), где 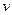 – скорость распространения волны, а Ф – одно из следующих полей: B,H,E,D. Уравнению (1) удовлетворяют плоские электромагнитные волны, то есть волны, которые описываются следующим уравнением:
– скорость распространения волны, а Ф – одно из следующих полей: B,H,E,D. Уравнению (1) удовлетворяют плоские электромагнитные волны, то есть волны, которые описываются следующим уравнением: 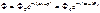 , где
, где  – временная фаза, а
– временная фаза, а  – пространственная фаза. Если эту функцию подставить в (1), волновое уравнение примет вид:
– пространственная фаза. Если эту функцию подставить в (1), волновое уравнение примет вид: 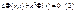 . Уравнение (2) называют уравнением Гельмгольца. Оно описывает пространственные характеристики гармонической волны в однородной среде. На этом уравнении базируется теория интерференции и дифракции. Рассмотрим классический опыт Юнга по интерференции от двух щелей. Сферическая волна из источника S падает на непрозрачный экран с одной щелью. Щель является источником вторичной сферической волны, интенсивность которой уже много меньше исходной. Полученная волна распространяется и падает, в свою очередь, на непрозрачный экран с двумя отверстиями, которые являются теперь источниками вторичных волн. Так как отверстия два, то и полученных волн тоже будет две. Данные волны обладают свойством когерентности, поэтому для них возможно явление интерференции.
. Уравнение (2) называют уравнением Гельмгольца. Оно описывает пространственные характеристики гармонической волны в однородной среде. На этом уравнении базируется теория интерференции и дифракции. Рассмотрим классический опыт Юнга по интерференции от двух щелей. Сферическая волна из источника S падает на непрозрачный экран с одной щелью. Щель является источником вторичной сферической волны, интенсивность которой уже много меньше исходной. Полученная волна распространяется и падает, в свою очередь, на непрозрачный экран с двумя отверстиями, которые являются теперь источниками вторичных волн. Так как отверстия два, то и полученных волн тоже будет две. Данные волны обладают свойством когерентности, поэтому для них возможно явление интерференции. 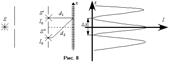 Основное противоречие здесь заключается в следующем: явление фотоэффекта и эффекта Комптона, казалось бы, довольно убедительно показали, что свет есть ничто иное, как поток корпускул. Тогда, так как интенсивность зависит от числа фотонов, то если освещать непрозрачный экран двумя лучами, по идее, интенсивность для каждой точки экрана должна быть выше, чем если бы его освещали только из одного источника. На деле же для некоторых участков экрана интенсивность, в соответствии с рис. 8, получается более низкой, а для других – более высокой, чем должна бы в соответствии с квантовой моделью. С точки зрения корпускулярной теории это явление объяснить нельзя. Однако, если ввести в рассмотрение волновую модель света, описанное явление получает замечательное объяснение с помощью явления интерференции. Таким образом, для света характерны корпускулярные и волновые свойства.
Основное противоречие здесь заключается в следующем: явление фотоэффекта и эффекта Комптона, казалось бы, довольно убедительно показали, что свет есть ничто иное, как поток корпускул. Тогда, так как интенсивность зависит от числа фотонов, то если освещать непрозрачный экран двумя лучами, по идее, интенсивность для каждой точки экрана должна быть выше, чем если бы его освещали только из одного источника. На деле же для некоторых участков экрана интенсивность, в соответствии с рис. 8, получается более низкой, а для других – более высокой, чем должна бы в соответствии с квантовой моделью. С точки зрения корпускулярной теории это явление объяснить нельзя. Однако, если ввести в рассмотрение волновую модель света, описанное явление получает замечательное объяснение с помощью явления интерференции. Таким образом, для света характерны корпускулярные и волновые свойства.
Опыт показывает, что картинка распределения интенсивности  результата интерференции в зависимости от координаты x имеет вид указанный на рис. 8 вид. Формально, характеризуя зависимость I(x), мы можем записать:
результата интерференции в зависимости от координаты x имеет вид указанный на рис. 8 вид. Формально, характеризуя зависимость I(x), мы можем записать:  (3). Здесь I0 – интенсивность источников S’ и S’’. Множитель 2 возникает вследствие того, что у нас два источника. В последней формуле
(3). Здесь I0 – интенсивность источников S’ и S’’. Множитель 2 возникает вследствие того, что у нас два источника. В последней формуле  (x) является разностью фаз между интерферирующими лучами в точке наблюдения. Найдём её. Запишем уравнения плоской волны для источников S’ и S’’:
(x) является разностью фаз между интерферирующими лучами в точке наблюдения. Найдём её. Запишем уравнения плоской волны для источников S’ и S’’:  и
и 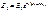 . Тогда
. Тогда  . Отсюда для корпускулярной интерпретации опыта Юнга возникают чрезвычайно большие трудности. Если каким-то образом приписать отдельному фотону фазу, тогда необходимо считать, что
. Отсюда для корпускулярной интерпретации опыта Юнга возникают чрезвычайно большие трудности. Если каким-то образом приписать отдельному фотону фазу, тогда необходимо считать, что  в (3) является разностью фаз двух фотонов, прошедших через различные щели. Но это противоречит закону сохранения энергии, поскольку два фотона при попадании в одну точку экрана выделяют энергию, не равную сумме их энергий. При некоторых условиях (cos
в (3) является разностью фаз двух фотонов, прошедших через различные щели. Но это противоречит закону сохранения энергии, поскольку два фотона при попадании в одну точку экрана выделяют энергию, не равную сумме их энергий. При некоторых условиях (cos  =-1) они могут взаимно уничтожить друг друга, при других (cos
=-1) они могут взаимно уничтожить друг друга, при других (cos  =1) – выделенная энергия в два раза больше, чем сумма энергий фотонов. Ясно, что такая интерпретация фазы неприемлема. Поэтому не представляется возможным приписать фотону характеристику, аналогичную фазе электромагнитной волны. Характеристика, аналогичная фазе волны, принадлежит не фотону, а состоянию, которое описывает его движение. Это значит, что интерференцию необходимо описать как явление, происходящее при наличии лишь одного фотона. Эксперименты с очень маленькими интенсивностями света, когда можно быть уверенным, что одновременно в образовании интерференционной картины участвует не более одного фотона, показали, что интерференционная картина образуется попаданием на экран отдельных фотонов. Это говорит о том, что движение отдельного фотона в интерференционных не зависит от наличия других. Фотон интерферирует сам собой. Вследствие этого говорят, что существует вероятность наблюдения фотона в тот или иной момент времени в той или иной точке пространства. Поэтому функция Ф из уравнения (2), описывающего распространение отдельного фотона, будет иметь смысл не, например, напряжённости электрического поля Е в данной точке пространства, а плотности вероятности нахождения фотона в данной точке пространства в данный момент времени t Таким образом, корпускулярное описание не позволяет говорить о движении фотона по какой-то траектории. Не имеет также смысла говорить, что фотон прошёл при интерференции через ту или иную щель.
=1) – выделенная энергия в два раза больше, чем сумма энергий фотонов. Ясно, что такая интерпретация фазы неприемлема. Поэтому не представляется возможным приписать фотону характеристику, аналогичную фазе электромагнитной волны. Характеристика, аналогичная фазе волны, принадлежит не фотону, а состоянию, которое описывает его движение. Это значит, что интерференцию необходимо описать как явление, происходящее при наличии лишь одного фотона. Эксперименты с очень маленькими интенсивностями света, когда можно быть уверенным, что одновременно в образовании интерференционной картины участвует не более одного фотона, показали, что интерференционная картина образуется попаданием на экран отдельных фотонов. Это говорит о том, что движение отдельного фотона в интерференционных не зависит от наличия других. Фотон интерферирует сам собой. Вследствие этого говорят, что существует вероятность наблюдения фотона в тот или иной момент времени в той или иной точке пространства. Поэтому функция Ф из уравнения (2), описывающего распространение отдельного фотона, будет иметь смысл не, например, напряжённости электрического поля Е в данной точке пространства, а плотности вероятности нахождения фотона в данной точке пространства в данный момент времени t Таким образом, корпускулярное описание не позволяет говорить о движении фотона по какой-то траектории. Не имеет также смысла говорить, что фотон прошёл при интерференции через ту или иную щель.
4. Дифракция рентгеновских лучей в кристаллах.
Дифракцией называют огибание волной препятствий, не связанное с явлениями отражения, преломления или рассеяния света. Дифракция является результатом интерференции вторичных волн
Дифракция волны на препятствии происходит всегда, независимо от размеров самого препятствия или длины волны. Когда размеры препятствия гораздо больше длины волны, дифракцию можно обнаружить на значительном удалении от препятствия. Если же длина волны соизмерима с размерами препятствия, то дифракцию можно наблюдать в непосредственной близости от препятствия. Длина волны рентгеновского излучения составляет 1 – 0,001 нм. Поэтому рассматривают дифракцию рентгеновского излучения на кристаллах. Кристаллами называется упорядоченная структура, в узлах которой находятся частицы. Рассмотрим на примере кристаллов поваренной соли. Параметр d определяет расстояние, начиная с которого строение решётки повторяется. d называют периодом кристаллической решётки. Cуществует возможность использовать кристаллическую решётку в качестве дифракционной. Если волна падает на кристалл в определённом направлении, то мы можем рассматривать процесс прохождение волны через кристалл как последовательные отражения её от кристаллических плоскостей. В этом случае ион становится источником вторичных волн. При этом часть луча отражается от ионов первой кристаллической плоскости, а другая часть проходит дальше. Так как угол падения равен углу отражения, то те фотоны, угол падения которых был одинаков, после отражения будут двигаться параллельно друг другу. Чтобы собрать их вместе, поставим на пути отражённого луча собирающую линзу. Тогда на экране, расположенном за линзой мы сможем наблюдать дифракционную картину. Как известно, интерференционный максимум или минимум определяются тем, приходят ли волны в данную точку синфазно или же в противофазе. Разность фаз двух лучей будет зависеть от расстояния, пройденного этими лучами.
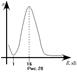


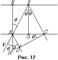 Дадим теперь явлению дифракции на кристалле некоторую количественную оценку. Отражённые лучи, как видно из рис. 11, будут иметь разность хода равную
Дадим теперь явлению дифракции на кристалле некоторую количественную оценку. Отражённые лучи, как видно из рис. 11, будут иметь разность хода равную  . Пусть лучи падают на кристалл под определённым углом
. Пусть лучи падают на кристалл под определённым углом  . Потребуем выполнения в точке наблюдения условия максимума интенсивности:
. Потребуем выполнения в точке наблюдения условия максимума интенсивности:  (
( ), где
), где  – произвольное целое положительное число. Увеличим часть рис. 11 чтобы рассмотреть его геометрию. Очевидно, что разность хода
– произвольное целое положительное число. Увеличим часть рис. 11 чтобы рассмотреть его геометрию. Очевидно, что разность хода  будет определяться следующим соотношением:
будет определяться следующим соотношением:  (1). Так как треугольники
(1). Так как треугольники  и
и  равны, то сторона
равны, то сторона  . Найдём её.
. Найдём её. 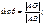
 . Нам известно, что
. Нам известно, что  – период кристаллической решётки. Тогда (2). Таким образом,
– период кристаллической решётки. Тогда (2). Таким образом,  (3). Рассмотрим теперь
(3). Рассмотрим теперь  . Угол
. Угол 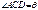 . Этот факт легко доказывается, если записать выражения для всех углов треугольника. Поэтому
. Этот факт легко доказывается, если записать выражения для всех углов треугольника. Поэтому 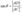
 . Таким образом,
. Таким образом,  или
или  . Так как
. Так как 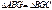 , то
, то  .Возвращаясь к выражению(1), с учётом последнего выражения, а также уравнения (3), мы можем записать:
.Возвращаясь к выражению(1), с учётом последнего выражения, а также уравнения (3), мы можем записать:  . Преобразуем последнее выражение:
. Преобразуем последнее выражение: 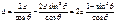 ;
; 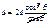 ,
,  (4). С другой стороны, разность фаз между волнами, отражёнными от соседних поверхностей, равна
(4). С другой стороны, разность фаз между волнами, отражёнными от соседних поверхностей, равна  . Так как мы требовали условие интерференционного максимума, то, в соответствии с формулой (
. Так как мы требовали условие интерференционного максимума, то, в соответствии с формулой ( ), мы можем записать:
), мы можем записать:  . Учитывая выражение для
. Учитывая выражение для  (4), получим:
(4), получим:  . По определению k=2(pi)/(Lambda). Подставляя это выражение в последнюю формулу,получим:(pi)*m=d*[2*(pi)/(Lambda)]*cos
. По определению k=2(pi)/(Lambda). Подставляя это выражение в последнюю формулу,получим:(pi)*m=d*[2*(pi)/(Lambda)]*cos  или, окончательно,
или, окончательно,  (5). Формула (5) называется
(5). Формула (5) называется  условием Вульфа – Брэгга. Она показывает, под каким углом на кристалл с заданным периодом кристаллической решётки должно падать излучение, чтобы было возможным наблюдение интерференционных максимумов. В тоже время, с помощью формулы (5) мы можем определить период кристаллической решётки исследуемого кристалла. Известно, что в случае объёмной кристаллической решётке, особенно острым будет центральный максимум, т. е. m= 1 (<= см. рис. 13). Поэтому, посылая на кристалл лучи под различными углами, мы при каком-то конкретном угле сможем наблюдать максимум. Зная угол, легко определить и период кристаллической решётки..
условием Вульфа – Брэгга. Она показывает, под каким углом на кристалл с заданным периодом кристаллической решётки должно падать излучение, чтобы было возможным наблюдение интерференционных максимумов. В тоже время, с помощью формулы (5) мы можем определить период кристаллической решётки исследуемого кристалла. Известно, что в случае объёмной кристаллической решётке, особенно острым будет центральный максимум, т. е. m= 1 (<= см. рис. 13). Поэтому, посылая на кристалл лучи под различными углами, мы при каком-то конкретном угле сможем наблюдать максимум. Зная угол, легко определить и период кристаллической решётки..
Метод Лауэ. Его суть заключается в том, что на кристалл ориентированный под определённым углом по отношению к лучу, падает пучок непрерывного излучения. Для излучения с некоторой длиной волны выполнится условие Вульфа – Брэгга. По интерференционной картине и геометрии опыта легко вычислить длину этой волны, а значит и период кристаллической решётки.
Метод Брэгга. Данный метод заключается в том, что монокристалл облучается монохроматическим рентгеновским излучением. При этом кристалл вращается вокруг оси кристаллографической зоны, ортогональной падающему пучку света так, что различные плоскости кристалла становятся последовательно в положение, соответствующее условию Вульфа – Брэгга. Для какого-то угла условие Вульфа – Брэгга будет выполнено. Зная угол, и результат интерференции, можно найти период кристаллической решётки. Так как излучение падает на различные кристаллические плоскости, то мы в случае сложного строения кристалла сможем полностью определить все расстояния между различными его плоскостями. Поэтому метод Брэгга используется, в основном, для анализа сложных кристаллических структур.
Метод Дебая – Шерера. В этом методе поликристалл или мелкий порошок из монокристаллических зёрен освещался монохроматическим излучением. Среди множества произвольно ориентированных монокристаллов всегда будут существовать такие, для которых будет выполнено условие Вульфа – Брэгга. Зная интерференционную картину, длину падающей волны и геометрию опыта, можно сделать заключение о строении кристалла.
Эффект Рамзауэра – Таунсенда.
В начале прошлого века Нем. физик Рамзауэр исследовал рассеяние электронов на атомах аргона при энергиях электрона от менее чем одного до нескольких десятков электрон-вольт. Обнаруженный им эффект назвали в последствии его именем. Он состоял в аномальной проницаемости некоторых газов (в частности аргона) для медленных электронов. Брался триод, в одной половине которого электроны не ускорялись, а в другой ускорялись. Трубку триода наполняли инертным газом (аргон). Электрон, попадая с раскалённой нити катода в пространство триода, движется по направлению к катоду и сталкивается с молекулой газа; при этом электрон рассеивается на ней. Поэтому, чем больше будет энергия электрона, тем больше шансов, что он пролетит без столкновения, то есть тем меньше вероятность рассеяния. Таким образом, с ростом ускоряющей разности потенциалов сила тока в цепи катод – анод должна возрастать. Графически зависимость между данными величинами можно представить так (см. рис. 17). Здесь зависимость P=P(E) есть зависимость вероятности рассеяния электрона от его энергии. Введём теперь в рассмотрение несколько новых величин, которые впоследствии помогут нам количественно описать эффект Рамзауэра. Будем рассматривать сечение рассеяния частиц. Понятие сечения рассеяния связано с вероятностью столкновения частицы с атомом или ядром. Будем считать частицу точечной. Пусть электрон падает на площадь  объёма, в котором расположены молекулы с концентрацией n0 (рис. 18). В слое толщиной dx в направлении движения электрона находится число молекул n0dV=n0sdx, а сумма их поперечных сечений, которая как бы закрывает собой часть площади S, равна ds=(сигма)n0sdx, где(сигма)-коэффициент пропорциональности.Отсюда следует, что вероятность попадания электрона в одну из молекул в слое dx будет равна:
объёма, в котором расположены молекулы с концентрацией n0 (рис. 18). В слое толщиной dx в направлении движения электрона находится число молекул n0dV=n0sdx, а сумма их поперечных сечений, которая как бы закрывает собой часть площади S, равна ds=(сигма)n0sdx, где(сигма)-коэффициент пропорциональности.Отсюда следует, что вероятность попадания электрона в одну из молекул в слое dx будет равна:  . Как видно из полученной формулы, коэффициент
. Как видно из полученной формулы, коэффициент  имеет размерность площади:, отсюда и назв-ание сечения рассеяния. Рассмотрим, как же можно найти сечение рассеяния. Пусть у нас есть поток частиц, движущихся в газообразной среде. Тогда, вследствие рассеяния, плотность потока частиц убывает на величину dl=-ldP. Если частица прошла путь dx, то dl(x)=-l(x)n0(сигма)dx. Решаем обыкновенное дифференциальное уравнение с разделяющимися переменными.
имеет размерность площади:, отсюда и назв-ание сечения рассеяния. Рассмотрим, как же можно найти сечение рассеяния. Пусть у нас есть поток частиц, движущихся в газообразной среде. Тогда, вследствие рассеяния, плотность потока частиц убывает на величину dl=-ldP. Если частица прошла путь dx, то dl(x)=-l(x)n0(сигма)dx. Решаем обыкновенное дифференциальное уравнение с разделяющимися переменными.
 ;
; 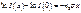 .
.  .
.
Последняя формула позволяет из опыта получить значение коэффициента рассеяния.
 Введём теперь понятие длины свободного пробега. Так называют расстояние, пройденное частицей между двумя последовательными соударениями. Увеличение длины свободного пробега электрона напрямую связано с уменьшением вероятности столкновения его с молекулой; уменьшением сечения рассеяния. Следовательно, возрастает вероятность пролёта электрона между катодом и анодом без соударения с молекулой, то есть возрастает ток в цепи катод – анод. Длина свободного пробега пропорциональна энергии электрона. Таким образом, зависимость (сигма)=(сигма)(E) будет иметь вид аналогичный указанному на первом из рисунков 17. Однако в действительности наблюдалась картина, указанная на рисунках 19 и 20. То есть при уменьшении энергии электрона от нескольких десятков электрон-вольт, сечение его рассеяния на аргоне растёт, как это и предсказывается теорией. Затем при энергии около 16 эВ поперечное сечение достигает максимума и при дальнейшем уменьшении энергии электрона уменьшается. При энергии электрона примерно 1 эВ сечение близко к нулю и затем начинает увеличиваться (см. рис. 20).
Введём теперь понятие длины свободного пробега. Так называют расстояние, пройденное частицей между двумя последовательными соударениями. Увеличение длины свободного пробега электрона напрямую связано с уменьшением вероятности столкновения его с молекулой; уменьшением сечения рассеяния. Следовательно, возрастает вероятность пролёта электрона между катодом и анодом без соударения с молекулой, то есть возрастает ток в цепи катод – анод. Длина свободного пробега пропорциональна энергии электрона. Таким образом, зависимость (сигма)=(сигма)(E) будет иметь вид аналогичный указанному на первом из рисунков 17. Однако в действительности наблюдалась картина, указанная на рисунках 19 и 20. То есть при уменьшении энергии электрона от нескольких десятков электрон-вольт, сечение его рассеяния на аргоне растёт, как это и предсказывается теорией. Затем при энергии около 16 эВ поперечное сечение достигает максимума и при дальнейшем уменьшении энергии электрона уменьшается. При энергии электрона примерно 1 эВ сечение близко к нулю и затем начинает увеличиваться (см. рис. 20).
Увеличение сечения с ростом энергии электрона и тем более почти полное исчезновение рассеяния вблизи энергии 1 эВ нельзя понять с точки зрения классических представлений, так как при этой энергии атомы аргона становятся как бы не существующими для электронов, и электроны пролетают сквозь них без столкновения. Объясняется это так. Электрону мы можем поставить в соответствие волну де Бройля  . Тогда при некоторой длине волны де Бройля (она, как известно, зависит от энергии электрона), будет наблюдаться дифракционный максимум или минимум. Здесь молекула газа является препятствием, на котором рассеивается электронная волна. Условие, при котором происходит хорошо выраженная дифракция таково, что длина падающей волны должна быть порядка диаметра атома. Тогда, если рассматривать оптическую аналогию, за препятствием возникает светлое пятно, а не тень. То есть электрон проходит сквозь атом без отклонения и сечение его рассеяния на атоме близко к нулю
. Тогда при некоторой длине волны де Бройля (она, как известно, зависит от энергии электрона), будет наблюдаться дифракционный максимум или минимум. Здесь молекула газа является препятствием, на котором рассеивается электронная волна. Условие, при котором происходит хорошо выраженная дифракция таково, что длина падающей волны должна быть порядка диаметра атома. Тогда, если рассматривать оптическую аналогию, за препятствием возникает светлое пятно, а не тень. То есть электрон проходит сквозь атом без отклонения и сечение его рассеяния на атоме близко к нулю
Понятие волн де Бройля...
В 1927 г. Луи де Бройль высказал предположение, что каждой движущейся частицы, мы можем поставить в соответствие некоторую длину волны. Подобную волну назвали в последствии волной де Бройля. Установим связь между параметрами волны и движущейся частицы.
1. Для волны де Бройля, как и для любой другой электромагнитной волны, мы можем записать:  (1). С другой стороны, для импульса:
(1). С другой стороны, для импульса:  ;
; 
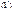 , где
, где  - волновой вектор. Но для волнового вектора мы можем записать:
- волновой вектор. Но для волнового вектора мы можем записать:  , т. о.
, т. о.  ;
;  . Из последней формулы следует выражение для волны де Бройля:
. Из последней формулы следует выражение для волны де Бройля:  (2). Из этого выражения следует интересный вывод, касающийся распределения интенсивностей в опытах с дифракцией электронов. Изменяя приложенную разгоняющую разность потенциалов, мы изменяем длину волны де Бройля. Когда выполняется условие Вульфа – Брэгга, возникает максимум.
(2). Из этого выражения следует интересный вывод, касающийся распределения интенсивностей в опытах с дифракцией электронов. Изменяя приложенную разгоняющую разность потенциалов, мы изменяем длину волны де Бройля. Когда выполняется условие Вульфа – Брэгга, возникает максимум.
2. 
 Определим теперь фазовый вид волн де Бройля. Введём некоторые дополнительные определения. Фазовой скоростью называют скорость, Vф с которой перемещается в пространстве фаза
Определим теперь фазовый вид волн де Бройля. Введём некоторые дополнительные определения. Фазовой скоростью называют скорость, Vф с которой перемещается в пространстве фаза  плоской монохроматической волны
плоской монохроматической волны  , где
, где  (3). Другими словами, фазовая скорость – это скорость распространения точки постоянной фазы волны. Найдём эту скорость. Рассмотрим для этого выражение (3). Это уравнение чисто геометрически описывает плоскость, перпендикулярную к оси
(3). Другими словами, фазовая скорость – это скорость распространения точки постоянной фазы волны. Найдём эту скорость. Рассмотрим для этого выражение (3). Это уравнение чисто геометрически описывает плоскость, перпендикулярную к оси  , на которой постоянна фаза волны. Таким образом, эта плоскость является как бы траекторией движения точки постоянной фазы. Поэтому, чтобы найти её скорость, необходимо взять производную от (3) по времени. Получим:
, на которой постоянна фаза волны. Таким образом, эта плоскость является как бы траекторией движения точки постоянной фазы. Поэтому, чтобы найти её скорость, необходимо взять производную от (3) по времени. Получим: 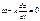 , так как производная от константы будет ноль. Отсюда найдётся и фазовая скорость:
, так как производная от константы будет ноль. Отсюда найдётся и фазовая скорость:  . Это соотношение определяет как раз фазовую скорость. Найдём некоторые свойства фазовой скорости. Возвращаясь к уравнениям
. Это соотношение определяет как раз фазовую скорость. Найдём некоторые свойства фазовой скорости. Возвращаясь к уравнениям  и
и  , выразим из них
, выразим из них  и
и  :
:  и
и 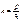 . Основываясь на определении фазовой скорости и полученных выражениях, найдём другую форму записи для неё:
. Основываясь на определении фазовой скорости и полученных выражениях, найдём другую форму записи для неё: 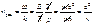 . Здесь
. Здесь  – фазовая скорость волны, соответствующей частице;
– фазовая скорость волны, соответствующей частице;  – скорость самой частицы;
– скорость самой частицы;  – скорость света. Таким образом, как видно из полученной формулы, фазовая скорость будет больше скорости света, однако никакого противоречия с теорией относительности это не вызывает. Очевидно, что фазовая скорость не измерима в эксперименте. Измерить можно лишь так называемую групповую скорость.
– скорость света. Таким образом, как видно из полученной формулы, фазовая скорость будет больше скорости света, однако никакого противоречия с теорией относительности это не вызывает. Очевидно, что фазовая скорость не измерима в эксперименте. Измерить можно лишь так называемую групповую скорость.
3. Групповой скоростью называют величину, приближённо характеризующую распространение негармонической волны (которая является суперпозицией группы гармонических волн). Если форма волны изменяется в результате дисперсии волн в среде не очень быстро, то можно рассматривать распространение негармонической волны как целого с групповой скоростью, отличной от фазовых скоростей её гармонических составляющих. Групповая скорость характеризует скорость переноса энергии волной. По определению для групповой скорости мы можем записать:  (отсюда сразу становится понятным условие, ограничивающее скорость изменения
(отсюда сразу становится понятным условие, ограничивающее скорость изменения  ). Возвращаясь к соотношениям, полученным для фазовой скорости, получим:
). Возвращаясь к соотношениям, полученным для фазовой скорости, получим:  . Таким образом,
. Таким образом,  .
.
4. Если волны распространяются в недиспрегирующей среде (фазовая скорость не зависит от частоты), то групповая скорость равна скорости движения частицы  . Тогда, вспоминая выражение для фазовой скорости
. Тогда, вспоминая выражение для фазовой скорости  , мы можем записать:
, мы можем записать:  . Из последней формулы следует:
. Из последней формулы следует:  .
.
 Итак, мы установили, как связаны свойства частиц и волн де Бройля. Оценим теперь длину волны де Бройля. В опытах Девисона – Джермера ускоряющая разность потенциалов была: 100В. Тогда для энергии электрона имеем выражение: Ee=eU. С другой стороны, кинетическая энергия электрона
Итак, мы установили, как связаны свойства частиц и волн де Бройля. Оценим теперь длину волны де Бройля. В опытах Девисона – Джермера ускоряющая разность потенциалов была: 100В. Тогда для энергии электрона имеем выражение: Ee=eU. С другой стороны, кинетическая энергия электрона  . На основании закона сохранения энергии необходимо положить
. На основании закона сохранения энергии необходимо положить  или
или  . Так как импульс электрона будет
. Так как импульс электрона будет  , то
, то 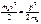 , то есть
, то есть  . Отсюда
. Отсюда  . Так как
. Так как  , то
, то  . Оценивая численное значение
. Оценивая численное значение  , мы можем получить, что
, мы можем получить, что  Å.
Å.

8. Опыт Франка-Герца. Атомные спектры.
Любое излучение электромагнитных волн осуществляется телами. Если излучение дискретно, то тело должно переходить с одного дискретного уровня на другой. Опыты Франка и Герца дали прямое доказательство дискретности атомных состояний. Если состояние атомных систем дискретно, а кинетическую энергию свободных электронов мы можем менять непрерывно, то при взаимодействии электронов с атомами, атомы могут поглощать энергию лишь строго определёнными порциями. В ходе опыта использовалась вакуумная лампа (см. рис.25). В ней находились накаливающийся катод, анод и две сетки, которые соединялись между собой. На сетку подавался ускоряющий потенциал  . Изменением его можно было плавно изменять кинетическую энергию электронов. На другую сетку подавался задерживающий потенциал
. Изменением его можно было плавно изменять кинетическую энергию электронов. На другую сетку подавался задерживающий потенциал  . Электроны, ускоренные между сеткой и катодом, попадали в свободное от полей пространство. Наблюдалась ВАХ, представленная на рисунке 26. Если теперь наполнить трубку парами (например, ртути) при пониженном давлении, в пространстве между сетками будут происходить столкновения электронов с атомами ртути. Те, что не потеряли энергию в результате подобных столкновений, достигнут анода. Те же, что энергию потеряли, анода не достигают. Анодный ток убывает. ВАХ лампы в этом случае представлена на рисунке 27. Качественно её можно объяснить следующим образом. Когда энергия электрона меньше разности энергий между энергетическими уровнями ртути, то оно не отдаёт энергию атому при столкновении. С увеличением ускоряющей разности потенциалов энергия электронов также возрастает. Когда разность потенциалов достигает 4,9 эВ., электроны при неупругом столкновении с атомами ртути вблизи сетки отдадут им всю свою энергию и уже не смогут преодолеть запирающей разности потенциалов. Следовательно, на анод могут попасть лишь
. Электроны, ускоренные между сеткой и катодом, попадали в свободное от полей пространство. Наблюдалась ВАХ, представленная на рисунке 26. Если теперь наполнить трубку парами (например, ртути) при пониженном давлении, в пространстве между сетками будут происходить столкновения электронов с атомами ртути. Те, что не потеряли энергию в результате подобных столкновений, достигнут анода. Те же, что энергию потеряли, анода не достигают. Анодный ток убывает. ВАХ лампы в этом случае представлена на рисунке 27. Качественно её можно объяснить следующим образом. Когда энергия электрона меньше разности энергий между энергетическими уровнями ртути, то оно не отдаёт энергию атому при столкновении. С увеличением ускоряющей разности потенциалов энергия электронов также возрастает. Когда разность потенциалов достигает 4,9 эВ., электроны при неупругом столкновении с атомами ртути вблизи сетки отдадут им всю свою энергию и уже не смогут преодолеть запирающей разности потенциалов. Следовательно, на анод могут попасть лишь
электроны не испытавшие неупругого столкновения, и поэтому при разности потенциалов 4,9В. сила тока начинает уменьшаться. Когда разность потенциалов достигает такого значения, что достаточное число электронов после неупругого столкновения смогут приобрести энергию, необходимую для преодоления задерживающего потенциала, начинается новый рост силы тока. При достижении разности потенциалов 9,8 В., электрон после одного неупругого столкновения приходит к сетке с энергией: 4,9 эВ., достаточной для второго неупругого столкновения. При втором неупругом столкновении электрон теряет всю свою энергию и не достигает анода. Поэтому сила тока начинает уменьшаться (второй максимум на ВАХ). Последующие максимумы объясняются аналогично. Из опыта следует, что разница в энергии основного состояния атома ртути и ближайшего возбуждённого состояния равна 4,9 эВ., что и доказывает дискретность состояний атомных систем.
Отношение энергии возбуждения атома к заряду электрона называется потенциалом ионизации:  . Первый потенциал возбуждения соответствует переходу атома с уровня с наименьшей энергией на последующий уровень.
. Первый потенциал возбуждения соответствует переходу атома с уровня с наименьшей энергией на последующий уровень.
Ионизацией называется процесс отрыва электрона от атома. Для определения потенциала ионизации также используют установку, изображённую на рисунке 25. Потенциал ионизации определяется по формуле  , где
, где  – работа выхода электрона из атома. Для атома водорода ВАХ этого процесса имеет вид, представленный на рисунке 28. Здесь измеряется ток, создаваемый положительными ионами. Величина 13,6 В. называется потенциалом насыщения.
– работа выхода электрона из атома. Для атома водорода ВАХ этого процесса имеет вид, представленный на рисунке 28. Здесь измеряется ток, создаваемый положительными ионами. Величина 13,6 В. называется потенциалом насыщения.






