Структура второй части статьи будет очень похожа.
1) Если ФУНКЦИЯ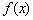 
умножается на число 
, то происходит растяжение её графика вдоль оси ординат.
Правило: чтобы построить график функции 
, где , нужно график функции 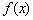растянуть вдоль оси 
в 
раз.
2) Если ФУНКЦИЯ умножается на число 
, то происходит сжатие её графика вдоль оси ординат.
Правило: чтобы построить график функции , где , нужно график функции 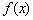сжать вдоль оси в 
раз.
Догадайтесь, какую функцию я буду снова пытать =)
Пример 11
Построить графики функций 
.
Берём синусоиду за макушку/пятки:
И вытягиваем её вдоль оси в 2 раза:
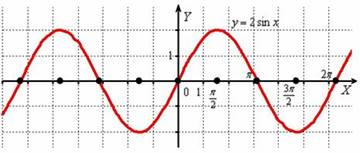
Период функции 
не изменился и составляет 
, а вот значения (все, кроме нулевых) увеличились по модулю в два раза, что логично – ведь функция умножается на 2, и область её значений удваивается: 
.
Теперь сожмём синусоиду вдоль оси в 2 раза:
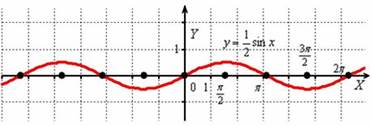
Аналогично, период не изменился, но область значений функции «сплющилась» в два раза: 
.
Нет, у меня нет какого-то пристрастного отношения к синусоиде, просто я хотел продемонстрировать, чем отличаются графики функций 
(Примеры №№1,3) от только что построенных собратьев . Постарайтесь ещё раз проанализировать и качественнее понять эти элементарные случаи. Даже минимальные знания о преобразованиях графиков окажут вам неоценимую помощь в ходе решения других задач высшей математики!
И, конечно же, классический пример растяжения/сжатия параболы:
Пример 12
Построить графики функций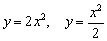 
.
Возьмём рога молодого оленя 
и вытянем их вверх вдоль оси в два раза: 
. Затем сожмём вдоль оси ординат в 2 раза: 
И снова заметьте, что значения функции увеличиваются в 2 раза, а значения 
уменьшаются во столько же раз (исключение составляет точка 
).
Отпустим в тундру удивлённое животное и продолжим изучать умножение функции на число: . Случаи 
не представляют интереса, поэтому рассмотрим отрицательные коэффициенты. Сначала распространённый частный случай 
:
Если ФУНКЦИЯ меняет знакна противоположный, то её график отображается симметрично относительно оси абсцисс.
Правило: чтобы построить график функции 
, нужно график 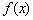отобразить симметрично относительно оси 
.
Пример 13
Построить график функции 
Отобразим синусоиду симметрично относительно оси :
Ещё более наглядно симметрия просматривается у следующей типовой функции:
Пример 14
Построить график функции 
График функции получается путём симметричного отображения графика 
относительно оси абсцисс:
Функции 
задают две ветви параболы, которая «лежит на боку». Обратная функция 
задаёт параболу целиком. С подобными графиками часто приходится иметь дело при нахождении площадей фигур, построении областей интегрирования двойных интегралов и в некоторых других задачах.
При умножении функции на отрицательное число , 
, построение графика следует выполнить в два этапа: сжатие (или растяжение) вдоль оси ординат, а потом – симметричное отображение относительно оси абсцисс. Конкретные примеры увидим в следующем топике.
