Для ефективного функціонування системи необхідно, щоб система мала певні властивості, які називаються показниками якості. До прямих показників якості належать: перерегулювання, час регулювання, коливальність та усталену похибку.
Під перерегулюванням розуміють максимальне відхилення регульованої величини від її усталеного значення в процесі регулювання і позначається 
(виражається у відносних одиницях або %).
Час регулювання 
- це мінімальний час після якого відхилення вихідної величини h(t) від її усталеного значення не буде перевищувати деяку наперед задану величину 
. Величина 
cкладає, як правило, 
5% від усталеного значення регульованої величини.
Час досягнення першого максимуму 
- це час, за який перехідна характеристика вперше досягає максимального значення.
Час першого узгодження 
- це час, за який перехідна характеристика вперше перетинає рівень усталеного значення.
Усталена похибка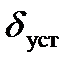 
- це різниця між заданим та дійсним значенням після закінчення перехідного процесу (в усталеному режимі).
Коливальністю перехідного процесу називають відношення амплітуд 
коливань двох послідовних періодів:
Рис. 8.1. Оцінка якості регулювання на основі перехідної характеристики
tр= 2,76 - час регулювання – це час після якого регульована величина не буде превищувати деякого наперед заданого значення 
, яке задається у відсотках від усталеного значення і рівне 5%. 
tм= 0,567 с - час першого максимуму– час за який регульована величина вперше досягає максимального значення.
δуст= 1-0,998 = 0,002 - усталена похибка– це різниця між дійсним иа заданим значення регульованої величини, що залишилась після закінчення перехідного процесу.
hmax= 1,57 - максимальне значення регульованої величини.
=0,998 - усталене значення вихідної регульованої величини.
- перерегулювання – характеризує максимальне відхилення регульованої величини від усталеного значення виражене у відсотках.
T0 = 1 c - період коливань.
A1 =0,57, A2 =0,21.
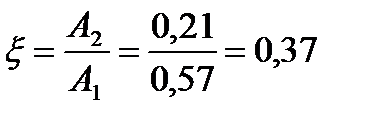-коливальність.
Кількість коливань на протязі часу регулювання: N=2.
Розрахована 
та змодельована 
перехідні характеристики наведені в таблиці, 
– абсолютна та відносна 
похибки аналітичного методу.
Таблиця 8.1.
Розрахунок абсолютної та відносної похибки
| t |
|
| 
| 
|
| 0,0088 | 0,0088 | |||
| 0,6 | 1,5552 | 1,5165 | 0,0387 | 2,55193 |
| 1,2 | 0,7499 | 0,7601 | 0,0102 | 1,34193 |
| 1,8 | 1,0575 | 1,0728 | 0,0153 | 1,42617 |
| 2,4 | 1,0195 | 1,0011 | 0,0184 | 1,83798 |
| 0,9591 | 0,9738 | 0,0147 | 1,50955 | |
| 3,6 | 1,0279 | 1,0209 | 0,007 | 0,68567 |
| 4,2 | 0,9820 | 0,9833 | 0,0013 | 0,13221 |
| 4,8 | 1,0038 | 1,0047 | 0,0009 | 0,08958 |
| 5,4 | 0,9976 | 0,9965 | 0,0011 | 0,11039 |
| 0,9966 | 0,9977 | 0,0011 | 0,11025 |
Можна зробити висновок, що визначенні перехідні характеристики аналітично та комп’ютерним методом співпадають. Це пояснюється похибкою неточності вимірювання, заокруглень числових значень і тому знайдені параметри різними методами незначно, але все ж таки відрізняються.
Максимальне значення відносної похибки 2,55193%, а її середнє значення - 1,50955%.
