Ссылки в пределах рабочего листа

 

Данные для вычислений по формуле могут непосредственно вводиться в формулу: = 2 + 3, а также считываться из других ячеек. Для доступа к данным в других ячейках рабочего листа используются ссылки. Ссылка является идентификатором ячейки или группы ячеек в книге.

В Excel различают ссылки трех типов: относительные, абсолютные, смешанные. Существуют два стиля оформления ссылок: стиль А1, или основной, и стиль R1C1.

Рассмотрим типы ссылок в стиле А1.

Относительная ссылка. При рассмотрении механизма относительных ссылок необходимо различать отображаемое и хранимое значения.

Хранимое значение относительной ссылки представляет собой смещение по столбцам и строкам от ячейки с формулой до адресуемой ячейки данных. Поэтому хранимое значение относительной ссылки не зависит от места расположения ячейки с формулой на листе и не изменяется при копировании и перенесении формул.

Отображаемое значение относительной ссылки представляет собой комбинацию из имени столбца и номера ячейки, соответствующую её текущим координатам. Отображаемое значение относительной ссылки автоматически изменяется при копировании формулы в новую ячейку.

Например, в формулах =А1+В1 и =А5+В5, находящихся в ячейках ВЗ и В7 (рис. 4а), отображаемым значениям А1 и А5 соответствуют одинаковые хранимые значения: <текущий столбец — 1><текущая строка — 2>.

 

 

а б

Рис. 4. Ссылки:

а) относительная; б) абсолютная

 

Если до момента фиксации ввода формулы нажимать на клавишу F4, можно изменить ссылку либо на абсолютную, либо на смешанную.

Абсолютная ссылка всегда указывает на зафиксированную при создании формулы ячейку или диапазон и не изменяется при переносе или копировании формулы в другую ячейку. Механизм абсолютной адресации включается в двух случаях:

– при записи знака $ перед именем столбца и номером строки (рис. 4б);

– при использовании имени ячейки.

Смешанные ссылки представляют собой комбинацию из относительных и абсолютных ссылок. Можно определить два типа смешанных ссылок:

1. Смешанная ссылка первого типа. В ссылках первого типа сим-вол $ стоит перед буквой, поэтому координата столбца рассма-тривается как абсолютная, а координата строки – как относитель-ная (рис. 5а).

2. Смешанная ссылка второго типа. В ссылках второго типа сим-вол $ стоит перед числом, поэтому координата столбца рассмат-ривается как относительная, а координата строки – как абсолют-ная (рис. 5б).

Примеры смешанных ссылок: =$B1+$D7, =B$1+D$7.

 

Рис. 5. Смешанные ссылки

 

Поиск решения

 

Инструмент Поиск решения применяется для решения задач, которые включают много изменяемых ячеек, и помогает найти комбинации переменных, которые устанавливают целевую ячейку в требуемое значение (например, максимальное или минимальное). Он также позволяет задать одно или несколько ограничений – условий, которые должны выполняться при поиске решений.

Ниже приведены примеры задач, которые могут быть решены с помощью средства Поиск решения – составление оптимального плана производства, рациона и плана перевозок.

Запуск надстройки «Поиск решения» осуществляется командой «Поиск решения» на ленте «Данные – Анализ» в версии Ехсеl 2007 или командой меню «Сервис – Поиск решения» в предыдущих версиях. Если команда недоступна, то следует выполнить активизацию надстройки «Поиск решения», установив соответствующий флажок в списке доступных надстроек (рис. 6). Окно подключения надстроек вызывается в версии Ехсеl 2007 последовательностью команд «Кнопка Office – Параметры Ехсеl – Надстройки (Управление: Надстройки Ехсеl) – Перейти» или командой меню «Сервис – Надстройки» в предыдущих версиях.

Планирование производства

Основная цель планирования любой деятельности - получение оптимального результата (максимальной прибыли, объема производства, минимальных издержек и т.п.) при имеющихся ограничениях. Разработке оптимальных программ (в смысле – планов) посвящен раздел математики под названием математическое программирование (не путать с представлением алгоритмов на языках программирования). Стандартная формулировка задачи математического программирования: требуется найти экстремум (минимум или максимум) целевой функции, наиболее полно характеризующей бизнес-процесс, при наложенных ограничениях. Допустимое решение, отвечающее этим условиям, называется оптимальным планом. Его может не существовать, если наложенные ограничения противоречивы, а иногда может существовать множество решений (разные планы приводят одинаковому результату). Если целевая функция и ограничения задаются линейными уравнениями, то такие задачи являются задачами линейного программирования.

 

 

Рис. 6. Окно подключения надстроек

 

Для решения задач линейного программирования используются различные методы (Ньютона, наискорейшего спуска, симплекс-метод), общий принцип которых сводится к следующему. Выбирается неоптимальный опорный план (изменяемые значения) и его параметры варьируются с целью последовательного улучшения плана, то есть оптимизации целевой функции с использованием надстройки «Поиск решения», что дает возможность решать оптимизационные задачи, не вникая в сложную математику.

Рассмотрим следующую задачу планирования производства.

Для изготовления двух видов продукции П1 и П2 используют четыре вида ресурсов Р1, Р2, Р3 и Р4. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице 1 (единицы измерения условные). Прибыль, получаемая от единицы продукции П1 и П2, – 2 и 3 руб. соответственно. Необходимо произвести поиск такого плана производства продукции, при котором прибыль от ее реализации будет максимальной.

Таблица 1

Вид ресурса	Запас ресурса	Число единиц ресурсов, затрачиваемых на изготовление единицы продукции
П1	П2
Р1
Р2
Р3
Р4

 

Решение начнем с составления математической модели задачи. Параметрами, значения которых требуется определить, является планируемое количество единиц каждого вида продукции П1 и П2. Обозначим эти параметры х ₁ и х ₂ соответственно. Тогда целевая функция F (суммарная прибыль от обоих видов продукции) определится следующей формулой:

F= 2 x ₁ + 3 x ₂. (1)

По смыслу задачи изменяемые параметры х ₁ и х ₂ должны быть целыми и неотрицательными. От них зависит не только прибыль, но и объем затрачиваемых ресурсов. Так как потребление ресурсов не должно превышать их запасов (табл. 1), то ограничения на потребление ресурсов выразится системой неравенств:

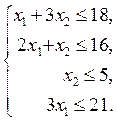(2)

Итак, математическая модель задачи: найти такой план выпуска продукции (подобрать целые неотрицательные х ₁ и х ₂), удовлетворяющий системе ограничений (2), при котором целевая функция (1) принимает максимальное значение.

Создадим соответствующую компьютерную модель в Ехсеl (рис. 7).

 

 

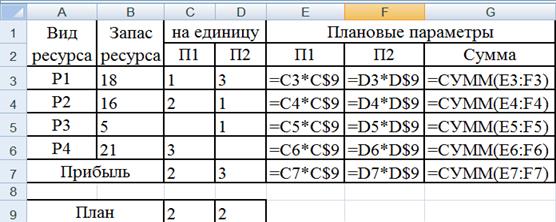
Рис. 7. Планирование производства

Теперь можно изменять значения ячеек C9:D9 и анализировать изменение требуемых ресурсов (G3:G6) и ожидаемой прибыли (G7). При запуске надстройки «Поиск решения» появляется диалоговое окно, в котором следует задать адрес целевой ячейки (G7), изменяемых ячеек (C9:D9), добавить ограничения (рис. 8).

 

 

Рис. 8. Задание исходных данных для окна Поиск решения

 

Можно уточнить модель, задав параметры поиска решения – неотрицательные значения (рис. 9). В таблице 2 приведено описание элементов этого окна. Следует отметить, что значения и состояния элементов управления, используемые по умолчанию, обычно достаточны для решения большинства задач.

 

 

Рис. 9. Задание параметров поиска решений

О результатах поиска решения можно узнать в появляющемся после выполнения расчётов окне (рис. 10).

При этом полученные численные значения оптимального плана будут находиться в изменяемых ячейках рабочего листа. В нашем случае это 6 и 4 единицы продукции П1 и П2.

 

 

Рис. 10. Результаты поиска решений

 

Таблица 2

Название	Описание
Поле Максимальное время	Определяет время, отпускаемое на решение задачи
Поле Предельное число итераций	Позволяет ограничить число промежуточных вычислений
Поле Относительная погрешность	Задает точность выполнения ограничений. Чем ближе значение к 1, тем ниже точность
Поле Допустимое отклонение	Служит для указания значения отклонения от оптимального решения (используется в задачах с целочисленными ограничениями)
Поле Сходимость	Когда относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа, указанного в поле Сходимость, поиск прекращается. Сходимость применяется только к нелинейным задачам
Флажок Линейная модель	Используется для поиска решения задач, в которых отсутствуют нелинейные зависимости. Нелинейные зависимости возникают при умножении одних изменяемых ячеек (переменных величин) на другие
Флажок Автоматическое масштабирование	Позволяет включить автоматическую нормализацию входных и выходных значений, качественно различающихся по величине, например, минимизация расходов в процентах по отношению к стоимостям, представленным в тысячах рублей
Флажок Показывать результаты итераций	Может быть использован для просмотра процесса нахождения решения
Группы Оценки, Разности, Метод поиска	Служат для выбора метода экстраполяции, метода численного дифференцирования и алгоритма оптимизации соответственно

Планирование закупок (рациона, задача о смесях)

Имеется два вида корма К1 и К2, содержащие питательные вещества (витамины) В1, В2 и В3. Содержание числа единиц питательных веществ в 1 кг каждого вида корма и необходимый минимум питательных веществ приведены в таблице 3. Стоимость 1 кг корма К1 и К2 равна 4 и 6 руб. соответственно. Необходимо составить план закупок (дневной рацион), имеющий минимальную стоимость, в котором содержание каждого вида питательных веществ было бы не менее установленного предела.

 

Таблица 3

Питательное вещество (витамин)	Необходимый минимум питательных веществ	Число единиц питательных веществ в 1 кг корма
К1	К2
В 1
В 2
В 3

 

Решение. За параметры х ₁ и х ₂ принимаем планируемое (изменяемое) количество кормов К1 и К2. Целевая функция F (суммарная стоимость обоих видов кормов) определится следующей формулой:

F= 4 x ₁ + 6 x ₂. (3)

Ограничения по количеству питательных веществ выразятся системой неравенств:

(4)

 

 

Рис. 11. Компьютерная модель в Ехсеl

 

Параметры поиска решения аналогичны предыдущей задаче. Главное отличие – установить целевую ячейку не максимальному, а минимальному значению. После выполнения поиска решения количества кормов К1 и К2 должны получиться значения 2 и 3 соответственно.

Планирование перевозок

Составьте оптимальный план перевозок бетонных изделий с трех заводов на четыре стройки. Считаем, что за один рейс машина перевозит одно бетонное изделие. Заданы мощности (планы) заводов, потребности строек и расстояния между заводами и стройками. Суммарная мощность заводов равна суммарной потребности строек. Холостые пробеги, состояние дорог и прочие факторы не учитываются. На рисунке 12 представлена компьютерная модель задачи.

 

	A	B	C	D	E	F
	Р а с с т о я н и я
		Стройка 1	Стройка 2	Стройка 3	Стройка 4	Планы заводов
	Завод 1
	Завод 2
	Завод 3
	Потребности строек
	План перевозок (число рейсов с заводов на стройки)	Вывезено с заводов
	Завод 1					=СУММ(B8:E8)
	Завод 2					=СУММ(B9:E9)
	Завод 3					=СУММ(B10:E10)
	Завезено на стройки	=СУММ(B8:B10)	=СУММ(С8:С10)	=СУММ(D8:D10)	=СУММ(Е8:Е10)
		Число рейсов * расстояния	Cуммарный
	Завод 1	=B8*B3				пробег
	Завод 2	Скопируйте формулу	всех машин
	Завод 3	в диапазон (B13:E15)	=СУММ(B13:E15)

 

Рис. 12. Компьютерная модель в Ехсеl

 

Запустите Поиск решения и заполните окна появившейся экранной формы (рис. 13).

Рис. 13. Экранная форма для запуска поиска решений

Целевая ячейка в данном случае – F15, в которой находится суммарный пробег машин со всех заводов на все стройки, и значение в которой надо сделать минимальным (или заданным, если надо «нагнать» план по километражу). Изменять можно ячейки B8:E10 (план перевозок) при условии равенства мощностей заводов и потребностей строек. Кроме того, следует задать условие, что количества рейсов – величины положительные и целые. После выполнения поиска решения в целевой ячейке должно получиться значение 65600.