Описание процессов распространения автоволн. Тау-модель распространения возбуждения

[3]

 

Математическое описание процессов распространения авто­волн [V.G.4] связано с решением достаточно сложных систем уравнений[Мф5]. Но для понимания процессов распространения автоволн можно воспользоваться достаточно простыми концептуальными моделями.

 

Мы будем использовать модель формальных активных сред, предложенную Н. Винером и А. Розенблютом, называемой τ-моделью [Мф6].

 

 

В τ-модели постулируется, что каждый элемент активной среды, может находиться в одномизтрех состояний (фазовых [V.G.7] состояний):

1. τ — возбуждение

2. R ‑ τ — «рефрактерный хвост»

Покой

 

 

Элемент в состоянии τ (возбуждения): · не может быть возбуждён соседним элементом · может возбудить соседний элемент, находящийся в состоянии покоя · уровень его мембранного потенциала выше критического уровня деполяризации (φм > φмпор).

 

Элемент в состоянии R ‑ τ («рефрактерного хвоста»): · не может быть возбуждён соседним элементом · не может возбудить соседний элемент, находящийся в состоянии покоя · уровень его мембранного потенциала ниже критического уровня деполяризации, но выше потенциала покоя (φмп > φм > φмпор).

 

Элемент в состоянии покоя: · может быть возбуждён соседним элементом (при условии, что трансмембранный потен­циал соседнего элемента выше значения порога рассматриваемого). · не может возбудить соседний элемент · уровень его мембранного потенциала равен потенциалу покоя (φм = φмп).

 

 

Обратите внимание на несоответствие постулатов τ-модели, представлениям об изменении возбудимости при возбуждении Н.Е.Введенского[Мф8]. Так состояние φмп > φм > φмпор после пика (спайка) возбуждения в τ‑модели мы характеризуем как состояние рефрактерности. А ранее мы говорили, что в этом состоянии возбудимая ткань находится в периоде экзальтации, т.е. повышенной возбудимости, поскольку снижен порог раздражения за счёт повышения уровня мембранного потенциала. Следует признать, что снижение порога раздражения в фазе следовой деполяризации потенциала действия далеко не всегда вызывает состояние экзальтации. Для этого, видимо, нужны дополнительные условия. Постулаты τ‑модели более соответствуют реальным явлениям.

 

Графическое представление τ‑модели[Мф9] показано на рис. 209251750.

 

Рис. 209251750. Графическое представление τ‑модели (с изменениями[Мф10]). R – рефрактерность. Клетка с темной штриховкой — элемент, находящиеся в состоянии возбуждения τ‑зона. Светлая штриховкой — клетки в состоя­нии (R ‑ τ) - рефрактерный хвост. Незаштрихованные клетки — элементы, находящиеся в покое. рис. 209251750.

 

В оригинале графическое представление τ‑модели[Мф11] несколько иной вид:

 

 

Допущения τ‑модели:

1. конфигурация потенциала действия упрощена [V.G.12]

2. не учитываются состояния относительной рефрактерности, а весь период R считается аб­солютно рефракторным или просто рефрактерным.

 

Из представленной модели следует, что возможны лишь три типа перехода элемента из одного фазового состояния в другое: 1. возбуждение ® рефрактерный хвост 2. рефрактерный хвост ® покой 3. покой ® возбуждение 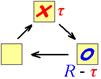    Рис. 209251751. Графическое представление фазовых переходов элементов в τ‑модели.   рис. 209251751.

 

Используя графическую модель, волну возбуждения можно представить в виде некото­рой зоны, состоящей из элементов, находящихся в рефрактерной фазе R, двигающейся по области покоящихся клеток с по­стоянной скоростью V (рис. 209251914).     Рис. 209251914. Плоская волна возбуждения. V – скорость движения волны, λ –длина волны.   Длина волны возбуждения λ, определяется соотношением, введенным Н.Винером: λ = R·V

 

Отсюда следует, что если рефрактерность элементов некоторого участка активной среды R1 повышена по сравнению с R2 (рис. 209260845), то и длина вол­ны возбуждения в этом участке будет больше: λ2 > λ1. 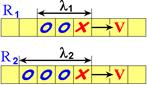    Рис. 209260845. Плоские волны возбуждения в активных средах разной рефрактерности.

 

Используя графическую модель, волну возбуждения можно представить в форме, показывающей изменение системы во времени (рис.709161046).     Рис.709161046. Распространение плоской волны возбуждения. S – место действия стимула (раздражителя).

 

Рис.709161118. Распространение плоской волны возбуждения от двух стимулов, нанесённых в разные моменты времени (t1 и t5). S – место действия стимула (раздражителя).

 

Основные свойства автоволн, касающиеся их распространения:

· распространяется без затухания.

· не интерферируют

· не отражаются от препят­ствий

· направление распространения определяется зонами рефрактерности и покоя.

 

Аннигиляция автоволн.

 

В однородных средах, в которых R и V одинаковы в любом участке, длина волны возбуждения постоянна.

В таких средах две встречные волны гасят друг друга, поскольку каждая из волн накладывается на невозбудимую зону встречной волны (рис. 209260850).

 

Рис. 209260850. Аннигиляция плоских автоволн.

 

Аналогично два встречных фронта пламени степного пожа­ра гасят друг друга. Позади огненного фронта каждого остает­ся черная, выжженная зона - зона рефрактерности, лишенная источников энергии.

В неоднородных средах процесс распространения автоволн усложняется.

Неоднородной называется активная среда, в различных участках которой значения R и V могут быть не одинаковыми. Активная среда организма, например миокард, неоднородна. В разных участках миокарда могут проходить кровенос­ные сосуды, нервные волокна и другие включения. При пато­логиях, например при возникновении зон некроза, свойства этих зон могут существенно отличаться и по рефрактерности R, и по скорости проведения волны V от этих параметров в уча­стках нормальной мышцы. Очевидно, что длины ав­товолн в различных участках неоднородных активных сред будут неодинаковыми. При выполнении определенных условий это может приводить к сердечным аритмиям, некоторые меха­низмы которых рассматриваются ниже.

Всегда ли движение автоволн навстречу друг другу заканчивается аннигиляцией? Нет. Рассмотри рис. 209260933.

 

 

Рис. 209260933. Пример прохождения одной автоволны через другую.

 

 

В реальных условиях приходится встречаться с ситуацией увеличение длины волны за счёт «рефрактерного хвоста», а не за счёт периода возбуждения.

 

Повышение рефрактерности среды приводит к нарушениям частоты и порядка возбуждения, но механизм этого нарушения другой.