Лемма Чебышева: Пусть среди значений случ. вел-ны Z нет отриц-х, тогда вер-ть того, что в некотором испытании значение этой случ. величины окажется больше, чем А (А-нек. число) оценивается по ф-ле: P(Z>A)£M(Z)/A; Равносильно утверждение: P(Z£A)³1-(M(Z))/A.
Неравенство Чебушева.: Вер-ть того, что в некотором испытании значение величины Yбудет отличаться от математического ожидания этой случайной величины не более чем на e (по абсолютной величине) оценивается по ф-ле:
Следствие 1). Пусть Y=(x1+…xn)/n, где х1,х2,…хn-независимы, M(xi)=ai, D(Xi)£C, где С- некоторое число i-1,2,…n, тогда справедливо нер-во. 
Следствие 2) Пусть имеется n независимых случайных х1,х2,хn чисел, имеющих одинаковые математические ожидания M(Xi)=a и дисперсиями, ограниченными числом С, тогда справедливы неравенства D(Xi)£C. 
Следствие 3) Пусть имеется n повторных независ. испытаний, в каждом из которых событие может произойти с … n. С каждой вер-тью число успехов n повторн. незав. Испыт. Х=m- биномиальный закон распределения. M(Xбин)=np; D(Xбин)=npq. Рассмотрим нер-во Чебышева: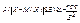 
, применим получится
Следствие 4) Для частости (доли) признака в повторных независимых испытаниях доля или частостьà X=m/n; M(m/n)=p; D(m/n)=pq/n. Применим нер-во Чебышева к этой случайной величине, получим:
; 
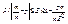-это также называется нер-вом Бернулли. Следствие 5) Устойчивость среднего арифметического. Практически достоверно можно утверждать, что при достаточно большом n среднее арифметическое случ. величины сколь угодно мало отличается от среднего арифметического их математических ожиданий. Предполагается независимость à
Говорят, что среднее число случайных величин сходится к вер-ти их математических ожиданий 
Замечание: Следствие 5 получается из следствия 1, если в правой части перейти к пределу при nà¥
Следствие 6) Устойчивость частости (доли) Практически достоверно, что доля успехов в n повторных независимых испытаниях сколь угодно мало отличается от их вер-ти успеха (при достаточно большом числе испытания n)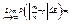 
,или
же 
Замечание: следствие 6 получ. Из следствия 4, если в правой части перейти к пределу при nà¥.
Вариационный ряд.
Пусть имеется некотор. признак Х,котор. подлежит изучению. Значение признака х назыв. их вариантами. Рассмотрим совокупность элементов – носителей признака. Кол-во элементов назыв. объемом совокупности.; Если признак х принимает изоли-
рованные значения, то он назыв. дискретным, если знач. Признака заполняют нек. интервал, то он интервальный. Пример: Х- размер обуви ß дискретный признак; Х- ростßинтервальный признак. Кол-во элементов совокупности, кот обладает данными значениями признака назыв. частотой этой варианты. Суммы всех частот = n. åni=n; (ni/n)=Wi.; Опр.: Вариационным рядом называется таблица, содержащая варианты в порядке возрастания и соответствующие им частоты или частости. Вариационный ряд – дискретный если варианты дискретны. Если признак принимает непрерывные
значения, то интервал его значения разбив. на частности соответствующими частотами или частостями – такой ряд –интервальный.
