Отчет по
ЧИСЛЕНННЫМ МЕТОДАМ
Выполнил: студент
гр. 411171
Сулейманова Д.И.
Проверила: доцент каф. хим.
кибернетики Кошкина Л.Ю.
Казань, 2012
Содержание
Тема 1. «Численное решение систем линейных алгебраических уравнений». 3
Постановка задачи. 3
Решение:
Прямые (точные) методы.. 3-4
Итерационные методы.. 5
Листинг программ. 4
Результаты.. 5
Выводы.. 5
Список литературы.. 5
ТЕМА 2. «ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ»
Постановка задачи
Решить систему линейных алгебраических уравнений:
A1:C3;E1:E3
| 0,5 | 1,7 | 0,3 | -0,24 | |
| 1,6 | 1,5 | -2,3 | 4,3 | |
| 3,7 | -2,5 | 3,2 | 6,5 |
0,5х1+1,7х2+0,3х3=-0,24
1,6х1+1,5х2-2,3х3=4,3
3,7х1-2,5х2+3,2х3=6,5
Для решения уравнения использовали следующие методы:
1. метод обратной матрицы,
2. метод Крамера,
3. метод Гаусса,
4. метод простых итераций,
5. метод Гаусса-Зейделя.
Решение:
Прямые (точные) методы
1) Метод обратной матрицы: ( х=А-1*В – формула данного метода, где В-вектор свободных членов, А-1-обратная функция)
А) Для реализации данного метода в электронных таблицах воспользовались математической функцией =МОБР(А1:С3) для определения коэффициента А:
| Коэффициент А | ||
| 0,035834 | 0,233488 | 0,16446 |
| 0,514126 | -0,01848 | -0,06148 |
| 0,360228 | -0,28441 | 0,074309 |
Б) Для выведения корней использовали функцию =МУМНОЖ(A5:C7;E1:E3).
2) Метод Крамера: (xi=∆i/∆, где ∆-главный определитель, ∆i-определитель, полученный путем замены i-го столбца столбцом свободных членов):
А) Замена столбцов главного определителя столбцом свободных членов:
| -0,24 | 1,7 |
| |
| 4,3 | 1,5 | -2,3 | |
| 6,5 | -2,5 | 3,2 | |
| 0,5 | -0,24 |
| |
| 1,6 | 4,3 | -2,3 | |
| 3,7 | 6,5 | 3,2 | |
| 0,5 | 1,7 |
| |
| 1,6 | 1,5 | 4,3 | |
| 3,7 | -2,5 | 6,5 |
Б) Нахождение ∆, ∆1, ∆2, ∆3 (∆ выражали через Д) функцией =МОПРЕД(A1:C3):
| =МОПРЕД(A1:C3) |
| Д |
| |
| Д1 |
| |
| Д2 |
| |
| Д3 | 21,909 |
В) Нахождение корней отношениями Д1/Д, Д2/Д, Д3/Д.
3) Метод Гаусса:
А) Прямой ход. Это приведение матрицы системы к треугольному виду.
Б) Обратный ход. Нахождение неизвестных.
Алгоритм метода Гаусса
n-количество уравнений.
Массивы: a(n,n)-коэффициенты системы; b(n)-свободные члены (правая часть уравнений); x(n)-решение системы.
| |
| FOR k=1 TO n-1 | |
| |
| FOR i=k+1 TO n | |
| |
| FOR j=k+1 TO n | |
| aij=aij-m*akj | |
| bi=bi-m*bk | |
| xn=bn/ann | |
| |
| FOR j=i+1 TO n | |
| S=∑aij*xi | |
| xi=(bi-s)/aii | |
| Печать xi |
Прямой ход
Обратный ход
| Цикл по уравнениям |
| Цикл по столбцам |
Выбор главного элемента и перестановка уравнений
| Определение № строки, в кот. находится макс.коэфф-т |
| g=k |
| FOR i=k+1 TO n |
| Если |aik|>|agk|, то g=i |
| FOR j=k TO n |
| z=agj; agj=akj; akj=z |
| z=bg; bg=bk;bk=z |
| Перестановка левых частей уравнений |
| Перестановка правых частей уравнений |
Итерационные методы
Для сходимости итерационного процесса достаточно, чтобы модули диагональных элементов были > или = суммы модулей не диагональных элементов:
| 3,7 | -2,5 | 3,2 | 6,5 | |
| 0,5 | 1,7 | 0,3 | -0,24 | |
| 1,6 | 1,5 | -2,3 | 4,3 |
1) Метод простых итераций:
А) Выразим х1, х2, х3 из уравнений главного определителя, тогда получим:
x1=(b1-a12x2-a13x3)/a11
x2=(b2-a21x1-a23x3)/a22
x3=(b3-a31x1-a32x2)/a33
Б) Зададим начальное (нулевое) приближение x1(0), x2(0), x3(0) . Подставляя их, получаем новое приближение.
В) Обозначим k-номер итерации, тогда для n уравнений итерационные формулы можно записать так:
xi(k)= 
(k-1))
Итерации проводятся до тех пор, пока не будет выполнено условие
|xi(k)-xi(k-1)|<e, i=1,2,… n.
Если условие не выполняется, итерации повторяются, приняв xi(k-1)= xi(k)
2) Метод Гаусса-Зейделя:
Этот метод представляет собой модификацию метода простых итераций, когда на k-той итерации при j<i xi уже вычислено на этой итерации, а расчетную формулу можно записать так:
xi(k)= 
(k)-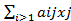 
(k-1))
Итерационный процесс продолжается до тех пор, пока не будет выполнено условие
|xi(k)-xi(k-1)|<e, i=1,2,… n.
Если условие не выполняется, итерации повторяются, приняв xi(k-1)= xi(k)
Алгоритм метода Гаусса-Зейделя
| Ввод n, e, a, b, x |
| Начало цикла |
| FOR i=1 TO n |
| FOR j=1 TO n |
S=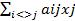 
|
| Xk=(bi-s)/aii |
S1=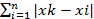 
|
| Xi=xk |
| Конец цикла, по условию s1<e |
| Печать xi |
n-количество уравнений; e-точность; a(n,n)-массив коэффициентов; b(n)-массив свободных членов; x(n)-массив решения. Вводится начальное приближение x(n).
Далее переходим в редактор Visual Basic (Сервис – Макрос – Редактор Visual Basic, Вставка – Модуль) и набираем программы по приведенным в лекциях алгоритмам [1].
Листинг программ
Sub metod_g()
n = 3
Dim a(1 To 3, 1 To 3)
Dim b(1 To 3)
Dim x(1 To 3)
For i = 1 To 3
For j = 1 To 3
a(i, j) = Worksheets("Лист2").Cells(i, j).Value
Next j
Next i
For i = 1 To 3
b(i) = Worksheets("Лист2").Cells(i, 5).Value
Next i
For k = 1 To n - 1
g = k
For i = k + 1 To n
If Abs(a(i, k)) > Abs(a(g, k)) Then g = i
Next i
For j = k To n
z = a(g, j): a(g, j) = a(k, j): a(k, j) = z
Next j
z = b(g): b(g) = b(k): b(k) = z
For i = k + 1 To n
m = a(i, k) / a(k, k)
For j = k + 1 To n
a(i, j) = a(i, j) - m * a(k, j)
Next j
b(i) = b(i) - m * b(k)
Next i
Next k
x(n) = b(n) / a(n, n)
For i = n - 1 To 1 Step -1
s = 0
For j = i + 1 To n
s = s + a(i, j) * x(j)
Next j
x(i) = (b(i) - s) / a(i, i)
Next i
For i = 1 To 3
Worksheets("Лист2").Cells(i, 9).Value = x(i)
Next i
End Sub
Sub MPI_SLAY()
n = 3
e = 0.0001
Dim a(1 To 3, 1 To 3)
Dim b(1 To 3)
For i = 1 To 3
For j = 1 To 3
a(i, j) = Worksheets("Лист3").Cells(i, j).Value
Next j: Next i
For i = 1 To 3
b(i) = Worksheets("Лист3").Cells(i, 5).Value
Next i
x10 = 0
x20 = 0
x30 = 0
Do
x1 = (b(1) - a(1, 2) * x20 - a(1, 3) * x30) / a(1, 1)
x2 = (b(2) - a(2, 1) * x10 - a(2, 3) * x30) / a(2, 2)
x3 = (b(3) - a(3, 1) * x10 - a(3, 2) * x20) / a(3, 3)
c = Abs(x1 - x10) + Abs(x2 - x20) + Abs(x3 - x30)
x10 = x1
x20 = x2
x30 = x3
k = k + 1
Loop While c > e
With Worksheets("Лист2")
.Range("J1").Value = x1
.Range("J2").Value = x2
.Range("J3").Value = x3
.Range("J5").Value = k
End With
End Sub
Sub GausZeid()
n = 3
e = 0.0001
Dim a(1 To 3, 1 To 3)
Dim b(1 To 3)
For i = 1 To 3
For j = 1 To 3
a(i, j) = Worksheets("Лист3").Cells(i, j).Value
b(i) = Worksheets("Лист3").Cells(i, 5).Value
Next j
Next i
x10 = 0: x20 = 0: x30 = 0
k = 0
Do
x1 = (b(1) - a(1, 2) * x20 - a(1, 3) * x30) / a(1, 1)
x2 = (b(2) - a(2, 1) * x1 - a(2, 3) * x30) / a(2, 2)
x3 = (b(3) - a(3, 1) * x1 - a(3, 2) * x2) / a(3, 3)
c = Abs(x1 - x10) + Abs(x2 - x20) + Abs(x3 - x30)
x10 = x1
x20 = x2
x30 = x3
k = k + 1
Loop While c > e
With Worksheets("Лист2")
.Range("K1").Value = x1
Range("K2").Value = x2
.Range("K3").Value = x3
.Range("K5").Value = k
End With
End Sub
Для запуска программ нажать на кнопку или на Run.
Полученный результат находится на Листе 2.
Результаты
| x1 | 2,064388 | 2,064388 | 2,064388 | 2,064429 | 2,064371 | |
| x2 | -0,60251 | -0,60251 | -0,60251 | -0,60252 | -0,60251 | |
| x3 | -0,82641 | -0,82641 | -0,82641 | -0,82638 | -0,82642 | |
| Методы | Обратной матрицы | Крамера | Гаусса | Простой итерации | Гаусса-Зейделя | |
Выводы
Системы линейных алгебраических уравнений можно решать как с помощью прямых, так и итерационных методов. Для систем уравнений средней размерности чаще используют прямые методы.
Итерационные методы применяют главным образом для решения задач большой размерности, когда использование прямых методов невозможно из-за ограничений в доступной оперативной памяти ЭВМ или из-за необходимости выполнения чрезмерно большого числа арифметических операций.
В данной работе мы рассмотрели 5 методов решения линейных алгебраических уравнений: метод обратной матрицы, Крамера, Гаусса, простой итерации и Гаусса-Зейделя. Первые 3 метода составляют группу прямых методов. Это аналитические методы, в них отсутствует погрешность метода, но погрешность вычислений неизбежна. Тем не менее, методы обратной матрицы и Крамера достаточно просты в алгоритме, тем более нами было найдено решение трехмерной матрицы (небольшая размерность), значения неизвестных сошлись. Что касается метода Гаусса, алгоритм данного метода достаточно громоздкий. Каждая следующая формула вычисления коэффициентов при преобразовании матрицы содержит результат предыдущей формулы, а значит и ее ошибку при вычислении. Наибольшее влияние на эту ошибку оказывает величина знаменателя (коэффициенты главной диагонали) – она не должна быть равна 0 и малой по абсолютной величине. В нашем случае таких предпосылок нет, метод Гаусса был осуществлен с выбором главного элемента, что дает малые невязки.
Итерационные методы простых итераций и Гаусса-Зейделя – схожи (одинаковы условия). Но погрешность метода Гаусса-Зейделя задается, погрешность вычислений не накапливается. Т.к. в формулах присутствуют величины из исходных уравнений. Недостатком метода по сравнению с прямыми методами является наличие итераций. Чем больше число итераций, тем больше требуется времени. Для метода простых итераций число итераций составляет 255, что на 234 больше чем число итераций для метода Гаусса-Зейделя, следовательно, применение данного метода для решения нашего уравнения не выгодно.
Нужно обратить внимание, что наша матрица имеет небольшую размерность, то есть для нахождения неизвестных в нашем случае можно воспользоваться прямыми методами, в частности методами обратной матрицы или Крамера. Алгоритм данных методов достаточно прост, не нужен выбор главного элемента, занимает меньше времени для решения.
Список литературы
1. Лекции по численным методам доцента кафедры химической кибернетики КНИТУ Кошкиной Л.Ю.
2. Кошкина Л.Ю. и др. Вычислительная математика в среде Excel: Методические указания. Часть 2. / Казан. гос. технол. ун-т; Казань, 2003, с. 72
3. Васильков Ю.В., Василькова Н.Н. Компьютерные технологии вычислений в математическом моделировании: Учебное пособие. – М.: Финансы и статистика, 2001.-256 с:ил.
4. Рено Н.Н. Численные методы. Учебное пособие / Казан. гос. технол. университет; Казань,2007, 112 с.
5. Турчак Л.И. Основы численных методов. - М.: Наука, 1987. – 318 с.
6. Дьяконов В.П. Справочник по алгоритмам и программам на языке бейсик для персональных ЭВМ: Справочник. – М.: Наука.1989. –240 с.
7. Назаров С.В., Мельников П.П. Программирование на MS Visual Basic: Учебное пособие / Под ред. С.В. Назарова. – М.: Финансы и статистика, 2001. – 320 с.: ил.
