Чтобы уменьшить избыточность, содержащуюся в ансамбле X источника информации, создается новый ансамбль Y символов, энтропия которой близка к максимальному значению. Затем с помощью элементов ансамбля Y составляются сообщения из ансамбля X.
Рассмотрим модель передачи информации с использованием кодера и декодера источника сообщений. Источник генерирует сообщения из ансамбля  , состоящего из элементов
, состоящего из элементов  ., образующих полную группу событий и появляющихся с некоторыми вероятностями
., образующих полную группу событий и появляющихся с некоторыми вероятностями  . Кодер источника использует ансамбль Y, состоящий из двух символов - (0, 1).
. Кодер источника использует ансамбль Y, состоящий из двух символов - (0, 1).
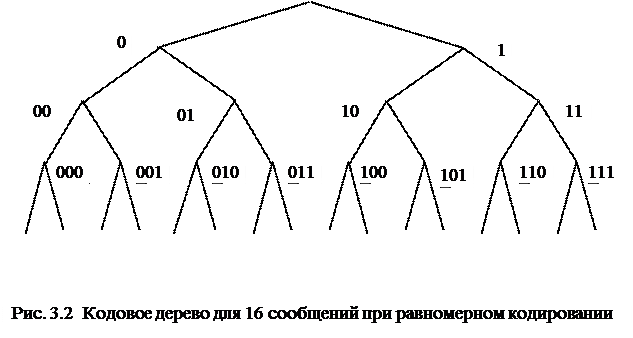
Существуют различные методы кодирования. Одним из них является метод, когда все элементы 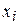 ансамбля X представлены одним и тем же числом элементов
ансамбля X представлены одним и тем же числом элементов
















ансамбля Y. Такое кодирование называется равномерным. Число возможных сообщений, которые кодируются двоичным  разрядным кодом, равно
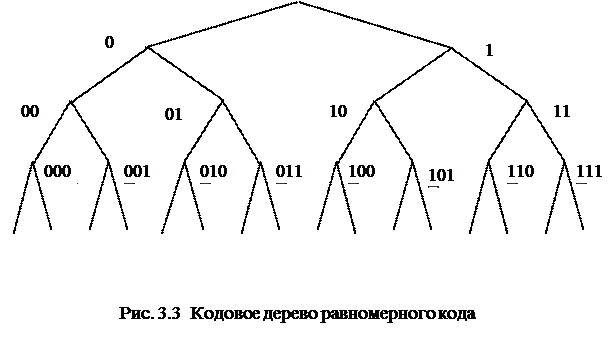
разрядным кодом, равно  . Например, при кодировании четырёхразрядным кодом можно закодировать 16 сообщений. Кодовое дерево (граф) изображено на рисунке 3.2.
. Например, при кодировании четырёхразрядным кодом можно закодировать 16 сообщений. Кодовое дерево (граф) изображено на рисунке 3.2.
Однако число кодируемых сообщений может быть меньше, чем  . Тогда используются не все коды и возникает избыточность при кодировании равномерным кодом. С другой стороны, не учитываются вероятности реализации сообщений
. Тогда используются не все коды и возникает избыточность при кодировании равномерным кодом. С другой стороны, не учитываются вероятности реализации сообщений  , составляющих ансамбль
, составляющих ансамбль  .
.
Пример 3.2. равномерного кодирования приведён в таблице 3.2. Все элементы ансамбля X расположены в первой колонке. Во второй колонке записаны вероятности реализаций соответствующих сообщений  . В третьей колонке количество информации, содержащееся в сообщении
. В третьей колонке количество информации, содержащееся в сообщении  . В четвёртой колонке представлены двоичные коды, соответствующие сообщениям
. В четвёртой колонке представлены двоичные коды, соответствующие сообщениям  . В пятой колонке записаны условные вероятности
. В пятой колонке записаны условные вероятности  появления символа «1» при реализации соответствующего сообщения
появления символа «1» при реализации соответствующего сообщения 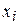
 ,
,
где  - общее число символов, употребляемых для кодирования
- общее число символов, употребляемых для кодирования  -го сообщения,
-го сообщения,
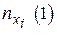 - число «1» в
- число «1» в  -ом сообщении.
-ом сообщении.
Для того чтобы закодировать двоичным кодом девять сообщений необходимо четыре двоичных разряда, (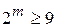 ; m = 4).
; m = 4).
| Таблица 3.2 | |||||
Анс-ль

| Вер. 
| 
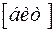
| Коды | Условн. вер.

| |

| 0.20 | 2.32193 | 1/4 | ||

| 0.2 | 2.32193 | 1/4 | ||
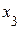
| 0.19 | 2.39593 | 2/4 | ||

| 0.15 | 2.73697 | 1/4 | ||

| 0.10 | 3.32193 | 2/4 | ||

| 0.08 | 3.64386 | 2/4 | ||

| 0.06 | 4.05889 | 3/4 | ||

| 0.01 | 6.64386 | 1/4 | ||

| 0.01 | 6.64386 | 2/4 | ||

|  2.79465 2.79465

| ||||
Кодовое дерево, отображающее коды при равномерном кодировании, представлено на рисунке 1.2.
Максимальная энтропия ансамбля X, в соответствии с теорией, равна
 = 3.16993
= 3.16993  .
.
Энтропия ансамбля X равна  =2.79465
=2.79465  .
.
Коэффициент избыточности ансамбля X равен
 =
=  = 0.881615,
= 0.881615,
коэффициент сжатия ансамбля X равен
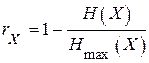 = 0.118385.
= 0.118385.
                 |
Рассмотрим ансамбль
 . Максимальная энтропия ансамбля Y равна
. Максимальная энтропия ансамбля Y равна
 = 1
= 1  .
.
Используя формулу полной вероятности, вычисляется вероятность  реализации символа «1» при кодировании элементов ансамбля X ‘символами ансамбля Y.
реализации символа «1» при кодировании элементов ансамбля X ‘символами ансамбля Y.
 = 0.375.
= 0.375.
Вероятность реализации символа «0» равна соответственно
 =0.625.
=0.625.
Количество информации, содержащееся в каждом символе ансамбля Y равно соответственно
 1.41504
1.41504 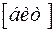 ,
, 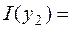 0.678072
0.678072 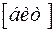 .
.
Энтропия ансамбля Y равна
 = 0.954434
= 0.954434  .
.
Соответственно коэффициент сжатия и коэффициент избыточности будут равны
 = 0.954434,
= 0.954434,  = 0.045566
= 0.045566
Из cравнения коэффициентов сжатия и коэффициентов избыточности ансамблей X и Y видно, произошло увеличение коэффициента сжатия и уменьшение избыточности ансамбля Y. Относительные величины равны соответственно
 = 1.0826,
= 1.0826,  = 2.59809.
= 2.59809.






