Рассмотрим модель канала передачи информации
, 
,
, 
[бит] - количество информации (мера неопределённости), содержащаяся в элементе 
ансамбля 
.
[бит] - количество информации, содержащееся в элементе при условии, на входе канала реализуется элемент ансамбля 
. Иногда её называют остаточной неопределённостью в элементе при условии реализации на входе канала элемента .
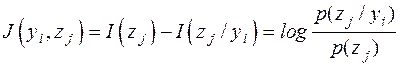[бит] - количество информации, содержащееся в элементе на выходе канала связи относительно элемента на входе канала. Используя безусловную и условную вероятности 
и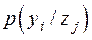 
, можно получить
- количество информации, содержащееся в элементе относительно элемента .
Суммируя 
по всем возможным элементам и с соответствующими весами 
, получим
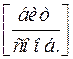(2.19)
- количество взаимной информации, содержащейся в ансамбле относительно ансамбля 
.
(Зюко. Помехоустойчивость и эффективность систем связи. «Связь». 1972, 360 с.)
Выразим количество взаимной информации через энтропии ансамблей:
= 
. (2.20 а)
Формулу (2.18 а) можно интерпретировать как среднее количество информации, переданное по каналу связи. Условная энтропия 
зависит от характеристик шума и интерпретируется как среднее количество информации, теряемое в канале связи из-за шума, и её называют ненадёжностью [ Р. Фано, стр 66].
Используя соотношение (2.17), можно показать
. (2.20 б)
Энтропия 
- это среднее количество принятой информации, необходимое для определения принятого сигнала. Условная энтропия 
- среднее количество принятой информации, когда известны вероятностные характеристики ансамбля Y. Ввиду того, что сигнал и шум аддитивны и независимы, а характеристики сигнала учитываются в расчетах условной энтропии , то - среднее количество информации, необходимое для определения помехи, или энтропия помехи (шума) в канале связи. При отсутствии помех в канале связи
= =0 и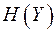 
= .
Пример 1. Положим, сигналы в канале передачи данных не искажаются, т.е. шумы в канале отсутствуют. Условная вероятность появления символов 
и 
в этом случае равна
Тогда условная энтропия 
равна нулю и количество взаимной информации определяется энтропией ансамбля Z. Но ранее было показано, что 
= 
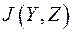. Из этого равенства и отсутствия шума следует, что 
, то есть количество взаимной информации на выходе канала связи относительно входа равна энтропии (неопределённости) ансамбля на входе канала передачи данных. И чем больше энтропия 
, тем больше информации передаётся по каналу связи.
Пример 2. Положим, сигналы в канале передачи данных искажаются настолько, что сигналы на приёмном конце канала передачи данных можно считать статистически независящими от передаваемых значений . В этом случае условная вероятность запишется как
и количество взаимной информации будет равно нулю, то есть абонент не получит никакой информации, хотя он будет фиксировать принимаемые символы .
Из рассмотренных примеров видно, чем больше энтропия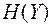 
, тем больше информации может быть передано по каналу. Для дискретных источников информации, как было показано ранее, энтропия принимает наибольшее значение, если элементы ансамбля равновероятны. Это положение относится как к ансамблю X, так и к ансамблям Y и Z то есть
, 
, где N и K – количество элементов ансамблей X и Y. Для непрерывных распределений вероятностей 
, 
, имеющих конечную дисперсию, энтропия принимает максимальное значение, если значения x и y распределены по нормальному закону.
Ансамбль сообщений, энтропия которых равна максимальному значению, является оптимальным ансамблем в смысле наибольшего количества передаваемой информации [Клюев].
Для оценки того, насколько отличается энтропия ансамбля от максимального значения вводится понятие коэффициента сжатия:
.
Из определения видно, что 
. При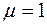 
каждое сообщение несёт максимальную информацию. Избыточность информации, содержащаяся в ансамбле, характеризуется коэффициентом избыточности
.
Чтобы уменьшить избыточность, содержащуюся в ансамбле X источника информации, создается новый ансамбль Y символов, энтропия которой близка к максимальному значению. Затем с помощью элементов ансамбля Y составляются сообщения из ансамбля X.
