Результат, полученный в предыдущем разделе подтверждается и при проверке гипотезы о включении переменных x1, x2, x4, x6 в уравнение. Следуя алгоритму проверки, рассчитывается 
«длинного» (с включением всех переменных) и «короткого» уравнения (без переменных, необходимость включения которых проверяется). Далее рассчитывается F-статистика:
и сравнивается с F критическим:
.
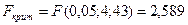Так как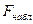 
< 
, гипотеза о незначимости факторов не отвергается, т.е. «короткое» уравнение лучше «длинного».
Итак, реализация алгоритмов пошагового исключения и пошагового включения привела к одному и тому же результату – модели, где в качестве объясняющих признаков использованы Х(3) (цена автомобиля, руб.) и Х(6) (стаж наименее опытного водителя, лет.).
Таблица 10 коэффициенты регрессии (2 фактора – 3 и 6)
Коэффициент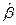 
0 в данном случае не имеет экономической интерпретации. Коэффициент 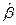3 показывает, что если стоимость автомобиля увеличится на 1 руб, то стоимость полиса КАСКО возрастет на 0,0015 долларов, а 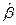6 показывает, что при росте стажа водителя, который будет вписан в страховку на 1 год, стоимость полиса снижается на 32,88 доллара.
Метод главных компонент.
Теперь проверим, улучшится ли качество модели, если строить регрессию на главных компонентах. Метод главных компонент – это один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации.
Сделав необходимые вычисления, получим матрицу факторных нагрузок:
| Матрица компонентa | ||||||
| Компонента | ||||||
| возраст авто, дней | -,404 | ,740 | ,161 | ,289 | -,423 | -,019 |
| пробег, км | -,306 | ,819 | ,207 | -,041 | ,434 | ,058 |
| цена авто, руб.(сс) | ,375 | ,079 | ,735 | -,545 | -,122 | -,045 |
| курс доллара | -,017 | -,433 | ,689 | ,570 | ,108 | ,016 |
| возраст младшего водителя, полных лет | ,928 | ,232 | -,047 | ,121 | -,075 | ,250 |
| стаж наименее опытного водителя, полных лет | ,867 | ,343 | -,106 | ,238 | ,091 | -,236 |
| Метод выделения: Анализ методом главных компонент. | ||||||
| a. Извлеченных компонент: 6 |
Таблица 11 Матрица компонент
Первая полученная компонента, состоящая из х5-возраста младшего водителя и х6- стажа наименее опытного водителя, интерпретируется как характеристики водителя, вторая - технические характеристики автомобиля, а третья – стоимость автомобиля (+курс доллара).
| Полная объясненная дисперсия | |||||||
| Компонента | Начальные собственные значения | Суммы квадратов нагрузок извлечения | |||||
| Итого | % Дисперсии | Кумулятивный % | Итого | % Дисперсии | Кумулятивный % | ||
| dimension0 | 2,010 | 33,501 | 33,501 | 2,010 | 33,501 | 33,501 | |
| 1,583 | 26,383 | 59,884 | 1,583 | 26,383 | 59,884 | ||
| 1,097 | 18,280 | 78,163 | 1,097 | 18,280 | 78,163 | ||
| ,778 | 12,968 | 91,131 | ,778 | 12,968 | 91,131 | ||
| ,408 | 6,803 | 97,934 | ,408 | 6,803 | 97,934 | ||
| ,124 | 2,066 | 100,000 | |||||
| Метод выделения: Анализ главных компонент. |
Таблица 12 объясненная дисперсия
По критерию Кайзера необходимо отобрать 3 первых фактора, так как у них собственные значения больше 1.
Теперь посмотрим, как полученные компоненты коррелируют со стоимостью полиса:
Таблица 13- корреляционная матрица новых компонент
Как видно из таблицы – всего двя коэффициента корреляции значимы. При этом связь и в первом и во втором случае достаточно заметная.
Результаты регрессии главных компонент:
| Коэффициентыa | ||||||
| Модель | Нестандартизованные коэффициенты | Стандартизованные коэффициенты | t | Знч. | ||
| B | Стд. Ошибка | Бета | ||||
| (Константа) | 1758,603 | 61,668 | 28,517 | ,000 | ||
| Характеристики водителя | -114,436 | 62,294 | -,229 | -1,837 | ,073 | |
| Технические характеристики автомобиля | -30,441 | 62,294 | -,061 | -,489 | ,627 | |
| Стоимость автомобиля | 237,586 | 62,294 | ,476 | 3,814 | ,000 | |
| R2 =0,283 R2adj =0,236 ст. ош. = 436 |
Таблица 14 результаты регрессии главных компонент
В получившейся регрессии на главных компонентах b1 и b2 не значимы и скорр намного ниже, чем в регресси на исходных переменных.
Таким образом, оптимальной моделью из всех рассчитанных представляется модель, где в качестве объясняющих признаков использованы факторы Х(3) (цена автомобиля, руб.) и Х(6) (стаж наименее опытного водителя, лет.).
Рассчитаем коэффициенты эластичности:
Это означает, что при росте цены автомобиля на 1%, цена полиса увеличивается на на 6,106 %.
Это означает, что при росте стажа наименее опытного водителя на 1% ВВП цена полиса падает на 1,73%.
В данной модели дисперсия стоимости полиса автострахования каско объясняется на 47,8 % - не очень высоким, но достаточным значением.
