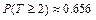Биномиальное распределение 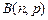 .
.
12.171 Дискретная случайная величина 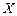 имеет биномиальное распределение
имеет биномиальное распределение 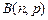 :
: 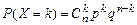 ,
, 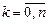 . Доказать, что:
. Доказать, что: 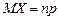 ,
, 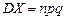 .
.
12.172 Найти математическое ожидание и дисперсию ДСВ 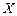 - числа отказов элемента некоторого устройства в десяти независимых опытах, если вероятность отказа элемента в каждом опыте равна
- числа отказов элемента некоторого устройства в десяти независимых опытах, если вероятность отказа элемента в каждом опыте равна 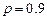 .
.
12.173 Найти дисперсию ДСВ 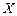 - числа появлений события
- числа появлений события 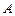 в двух независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы и известно, что
в двух независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы и известно, что 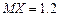
12.174 Производятся независимые испытания с одинаковой вероятностью появления события 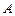 в каждом испытании. Найти вероятность появления события
в каждом испытании. Найти вероятность появления события 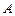 в одном испытании, если дисперсия числа появлений этого события в трёх независимых испытаниях равна
в одном испытании, если дисперсия числа появлений этого события в трёх независимых испытаниях равна 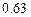 .
.
12.175 По одному из тиражей денежно-вещевой лотереи куплено 100 билетов. Среднее квадратичное отклонение числа выигравших билетов равно 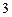 . Найти вероятность выигрыша по одному билету лотереи.
. Найти вероятность выигрыша по одному билету лотереи.
12.176 Вероятность того, что при трёх выстрелах стрелок попадёт в цель, хотя бы один раз, равна 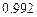 . Найти
. Найти 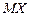 и
и 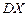 случайной величины
случайной величины 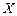 - числа попаданий при 20 выстрелах.
- числа попаданий при 20 выстрелах.
Распределение Пуассона 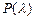 .
.
12.177 Дискретная случайная величина 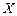 имеет распределение Пуассона
имеет распределение Пуассона 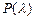 :
: 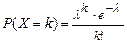
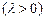 ,
, 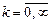 . Доказать, что:
. Доказать, что: 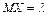 ,
, 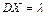 .
.
12.178 В течение часа на станцию скорой помощи поступает случайное число вызовов 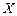 , распределённое по закону Пуассона с параметром
, распределённое по закону Пуассона с параметром 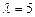 . Найти вероятности того, что в течение часа поступят: а) ровно два вызова; б) не более двух вызовов; в) не менее двух вызовов (Указание: принять
. Найти вероятности того, что в течение часа поступят: а) ровно два вызова; б) не более двух вызовов; в) не менее двух вызовов (Указание: принять 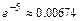 )
)
12.179 Число вызовов, поступающих на АТС (автоматическая телефонная станция) каждую минуту, распределено по закону Пуассона с параметром 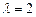 . Найти вероятности того, что минуту на АТС поступят: а) ровно три вызова; б) хотя бы один вызов; в) менее пяти вызовов (Указание: принять
. Найти вероятности того, что минуту на АТС поступят: а) ровно три вызова; б) хотя бы один вызов; в) менее пяти вызовов (Указание: принять 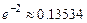 ).
).
12.180 Вероятность, что в течение часа на станцию скорой помощи не поступит ни одного вызова, равна 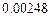 . Считая, что число вызовов
. Считая, что число вызовов 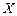 , поступающих в течение часа на станцию, имеет распределение Пуассона, найти её математическое ожидание
, поступающих в течение часа на станцию, имеет распределение Пуассона, найти её математическое ожидание 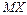 и дисперсию
и дисперсию 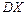 .
.
Геометрическое распределение 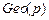 .
.
12.181 Дискретная случайная величина 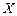 имеет геометрическое распределение
имеет геометрическое распределение 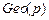 :
: 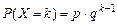 ,
, 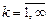 . Доказать, что:
. Доказать, что: 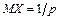 ,
, 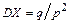 .
.
12.182 Производятся многократные испытания некоторого элемента на надёжность до тех пор, пока элемент не откажет. Вероятность отказа элемента в каждом испытании равна 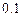 . Составить закон распределения ДСВ
. Составить закон распределения ДСВ 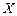 - числа произведённых опытов и найти её математическое ожидание и дисперсию.
- числа произведённых опытов и найти её математическое ожидание и дисперсию.
12.183 Вероятность поражения цели равна 0.05. Производится стрельба по цели до первого попадания. Составить закон распределения ДСВ 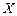 - числа произведённых выстрелов и найти вероятность того, что для поражения цели потребуется сделать не менее пяти выстрелов.
- числа произведённых выстрелов и найти вероятность того, что для поражения цели потребуется сделать не менее пяти выстрелов.
12.184 В большой партии изделий вероятность брака равна 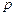 . Контроль качества проводится до первого появления бракованного изделия. В результате серии проверок обнаружено, что бракованное изделие впервые появлялось в среднем при десятом испытании. Найти вероятность брака
. Контроль качества проводится до первого появления бракованного изделия. В результате серии проверок обнаружено, что бракованное изделие впервые появлялось в среднем при десятом испытании. Найти вероятность брака 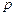 .
.
Равномерное распределение 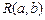 .
.
12.185 Непрерывная случайная величина 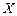 имеет равномерное распределение
имеет равномерное распределение 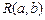 :
: 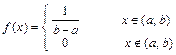 . Доказать, что
. Доказать, что 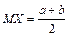 ,
, 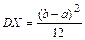 .
.
12.186 Автобусы некоторого маршрута идут строго по расписанию. Интервал движения 15мин. Найти вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус не более 5мин.
12.187 Цена деления шкалы измерительного прибора равна 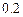 . Показания прибора округляют до ближайшего целого деления. Найти вероятность того, что при отсчёте будет сделана ошибка: а) меньшая
. Показания прибора округляют до ближайшего целого деления. Найти вероятность того, что при отсчёте будет сделана ошибка: а) меньшая 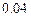 ; б) большая
; б) большая 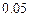 .
.
12.188 Шкала рычажных весов, установленных в лаборатории, имеет цену деления 1 г. При измерении массы химических компонентов смеси отсчёт делается с точностью до целого деления с округлением в ближайшую сторону. Какова вероятность, что величина 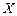 - возможная ошибка определения массы по абсолютной величине не превысит величины среднего квадратичного отклонения возможных ошибок определения массы
- возможная ошибка определения массы по абсолютной величине не превысит величины среднего квадратичного отклонения возможных ошибок определения массы 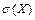 .
.
12.189 Непрерывная случайная величина 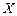 имеет равномерное распределение на интервале
имеет равномерное распределение на интервале 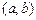 , причём
, причём 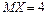 ,
, 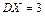 . Найти неизвестные постоянные
. Найти неизвестные постоянные 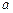 и
и 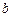 .
.
Показательное распределение 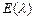 .
.
12.190 Непрерывная случайная величина 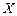 имеет показательное распределение
имеет показательное распределение 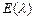 :
: 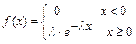
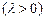 . Доказать, что
. Доказать, что 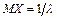 ,
, 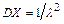 .
.
12.191 Непрерывная случайная величина 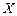 имеет показательное распределение:
имеет показательное распределение: 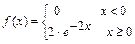 . Найти вероятность того, что
. Найти вероятность того, что 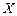 примет значение, меньшее математического ожидания
примет значение, меньшее математического ожидания 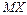 .
.
12.192 Длительность времени 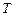 безотказной работы элемента имеет показательное распределение
безотказной работы элемента имеет показательное распределение 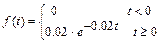 . Вычислить вероятности того, что за время длительностью
. Вычислить вероятности того, что за время длительностью 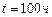 элемент: а) выйдет из строя; б) будет работать.
элемент: а) выйдет из строя; б) будет работать.
12.193 Испытывают два независимо работающих элемента. Длительность времени безотказной работы первого элемента имеет показательное распределение 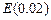 , второго -
, второго - 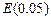 . Найти вероятность того, что за время длительностью
. Найти вероятность того, что за время длительностью 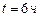 : а) оба элемента выйдут из строя; б) оба элемента будут работать; в) только один элемент выйдет из строя;
: а) оба элемента выйдут из строя; б) оба элемента будут работать; в) только один элемент выйдет из строя;
г) хотя бы один элемент выйдет из строя.
Время ожидания у бензоколонки АЗС является случайной величиной, распределённой по показательному закону со средним временем ожидания, равным. Найти вероятности следующих событий: а); б).
12.195 Дисперсия показательно распределённой случайной величины 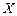 равна
равна 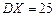 . Найти вероятность
. Найти вероятность 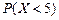 .
.
12.196 Время 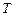 (в годах) непрерывной работы электрической лампочки имеет показательное распределение.
(в годах) непрерывной работы электрической лампочки имеет показательное распределение. 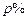 -ным ресурсом элемента называется такое число
-ным ресурсом элемента называется такое число 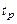 , что за время
, что за время 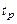 элемент не выходит из строя с вероятностью
элемент не выходит из строя с вероятностью 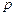 . Найти вероятность того, что лампочка будет гореть в течение 2 лет, если её 90%-ный ресурс составляет 6 месяцев.
. Найти вероятность того, что лампочка будет гореть в течение 2 лет, если её 90%-ный ресурс составляет 6 месяцев.
Ответы:
А); б); в). 12.179 а); б); в). 12.180,.
12.182,.
12.183 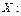
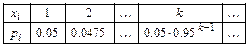
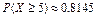
12.184 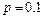 12.186
12.186 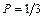 12.187 а)
12.187 а) 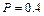 ; б)
; б) 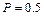 . 12.188
. 12.188 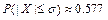 12.189
12.189 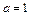 ,
, 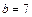 . 12.191
. 12.191 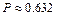 12.192а)
12.192а) 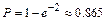 ; б)
; б) 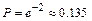 . 12.193а)
. 12.193а) 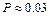 ; б)
; б) 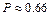 ; в)
; в) 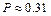 ; г)
; г) 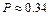 . 12.194а)
. 12.194а) 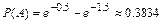 ; б)
; б) 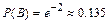 . 12.195
. 12.195 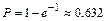 12.196
12.196