Дискретные случайные величины: законы распределения и числовые характеристики.
В задачах 12.131-12.136 требуется: а) составить закон распределения дискретной случайной величины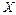 
и построить многоугольник полученного распределения; б) вычислить математическое ожидание 
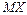и дисперсию 
.
12.131 Устройство состоит из трёх независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0.1. Случайная величина 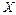- число отказавших элементов в одном опыте.
12.132 В партии из 10 деталей имеется 8 стандартных. Наудачу отобраны две детали. Случайная величина 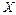- число стандартных деталей среди отобранных.
12.133 В урне 6 белых и 4 чёрных шара. Из неё три раза подряд извлекают шар, причём каждый раз вынутый шар возвращают в урну и шары перемешивают. Случайная величина 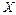- число извлечённых белых шаров.
12.134 Два стрелка независимо друг от друга делают по одному выстрелу в мишень. Вероятность попадания в мишень для первого стрелка – 0.8, для второго – 0.9. Случайная величина 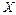- суммарное число попаданий в мишень.
12.135 Стрелок ведёт стрельбу по цели с вероятностью попадания при каждом выстреле 0.8. За каждое попадание он получает 5 очков, а в случае промаха очков ему не начисляют. Произведено три выстрела. Случайная величина 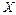- число очков, полученных стрелком.
12.136 Рабочий обслуживает три станка. Вероятность того, что станок в течение времени 
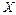потребует внимания рабочего, для первого станка равна 0.1, для второго – 0.2, для третьего – 0.3. Случайная величина - число станков, не требующих внимания рабочего в течение времени .
12.137 Дискретная случайная величина 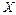задана рядом распределения 
. Найти значение её функции распределения 
Известны математические ожидания и дисперсии независимых случайных величин и:,,,. Найти математическое ожидание и дисперсию случайной величины, если: а); б).
12.139 Дискретная случайная величина 
принимает три возможных значения: 
с вероятностью 
; 
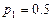с вероятностью 
и 
с вероятностью 
. Найти и , зная, что 
.
12.140 Дан перечень возможных значений дискретной случайной величины : 
, 
, 
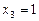, а также известны математические ожидания этой величины и её квадрата: 
, 
. Найти закон распределения величины .
12.141 Дискретная случайная величина Х имеет только два возможных значения: 
(
). Вероятность, что Х примет значение 
, равна 0.2. Найти закон распределения Х, зная, её математическое ожидание 
и среднее квадратичное отклонение 
12.143 Вероятность сдать экзамен по «Теории вероятностей» студентом на «5» равна 0.3; на «4» - 0.4. Найти вероятности получения оценок «2» и «3», если известно, что средний балл, получаемый студентами на экзамене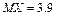 
.
Известны математические ожидания и дисперсии независимых случайных величин и:,,,. Найти математическое ожидание случайной величины, если: а); б).
12.145 Распределение дискретной случайной величины 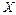определяется формулами: 
, 
. Требуется найти: а) неизвестную постоянную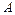 
; б) 
.
Ответы:
12.131 
, 
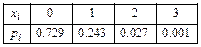
12.132 
, 
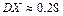
12.133 
, 
12.134 
, 
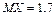12.135 
, 
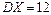
12.136 
, 
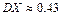
12.137 
12.138 а) 
; б) 
. 12.139 
, 
.
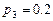12.140 
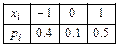12.141 
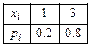12.143 
, 
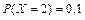А); б). 12.145 а); б).
