МИНИСТЕРСТВО НАУКИ И ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра технологии нефти и газа
ЛАБОРАТОРНАЯ РАБОТА 1.
РАСЧЕТ ФАЗОВОГО РАВНОВЕСИЯ МНОГОКОМПОНЕНТНОЙ СМЕСИ УГЛЕВОДОРОДОВ В СИСТЕМЕ ПАР-ЖИДКОСТЬ
ВАРИАНТ №21
Выполнил: ТП-05-01 Нафиков Р. А.
Проверил: Яковлев А. А.
УФА 2009
Цель работы – на примере расчета температуры верха ректификационной колонны рассмотреть:
алгоритм решения задач поиска корней нелинейной алгебраической математической модели;
обоснование правильности решения задачи
оценку быстродействия различных алгоритмов решения;
получение зависимости температуры верха от давления в изучаемом диапазоне давлений как основы для формирования закона регулирования работы верхней части ректификационной колонны.
Исходные данные:
Вариант 21
Базовое давление, Р0, ата 2,9
Компоненты системы 5 (бензол)
11 (м-ксилол)
10 (о-ксилол)
7 (толуол)
12 (п-ксилол)
Содержание компонентов в системе Y(1) 0,80
Y(2) 0,05
Y(3) 0,03
Y(4) 0,03
Y(5) 0,09
Коэффициенты уравнения Антуана
Бензол А 4,03129
В 1214,645
С 221,205
М-ксилол А 4,12768
В 1461,925
С 215,073
О-ксилол А 4,11810
В 1474,679
С 213,686
Толуол А 4,07427
В 1345,087
С 219,516
П-ксилол А 4,11103
В 1454,328
С 215,411
Ход работы
В ходе лабораторной работы использовались два основных метода расчета корня математической модели в форме алгебраического уравнения:
- метод половинного деления;
- метод хорд.
В данном случае нам необходимо рассчитать температуру верха ректификационной колонны. Этот расчет ведется из условия однократного испарения
∑(Y(i)/K(i))=1, (1)
где Y(i) – концентрация i-го компонента в парах, отводимых из колонны, мольные доли;
K(i) – константа фазового равновесия i-го компонента;
N – число компонентов смеси.
K(i)=P(i)/P0, (2)
где P(i) – давление насыщенных паров соответствующего компонента, ата;
P0 – давление верха колонны, ата.
Величины P(i) для углеводородов часто рассчитывают по уравнению Антуана:
lgP(i)=A(i)-B(i)/(C(i)+t), (3)
где А(i), B(i),C(i) – константы уравнения Антуана;
t – температура, оС.
Решение обратной (3) задачи
t=B(i)/(A(i)-lgP0)-C(i), (4)
позволяет рассчитать температуру кипения i-го компонента при давлении Р0.
Уравнение (1) является нелинейным и решается итерационными методами, в частности, методами половинного деления и хорд, после преобразования его в форму:
Z=(∑(Y(i)/K(i)))-1=0. (5)
Рассмотрим основы расчета по обоим методам:
1. Метод половинного деления.

Рисунок 1. Пояснительный график к расчету по методу половинного деления.
Порядок расчета по методу половинного деления следующий:
1. Рассчитываются температуры кипения компонентов смеси при заданном давлении Р0 по уравнению (4). Определяем максимальное и минимальное значение температуры и задаем исследуемые интервал [t1;t2]. Определяем Z1=f(t1) и Z2=f(t2).
2. Вычисляется
t=(t1+t2)/2 (6)
3. Определяются величины P(i) и K(i) по уравнениям (3) и (2).
4. Определяется значение функции Z по уравнению (5), если |t-t2|<ε, то t – корень уравнения.
5. При |t-t2|>ε, если Z*Z1<0, то полагаем t2=t, Z2=Z, иначе полагаем t1=t, Z1=Z. Процесс деления отрезка продолжается, возвращаясь к шагу 2, пока число итераций не превысит заданное значение максимального числа итераций.
2. Метод хорд.

Рисунок 2. Пояснительный график к расчету по методу хорд.
Порядок расчета по методу хорд следующий:
1. Рассчитываются температуры кипения компонентов смеси при заданном давлении Р0 по уравнению (4). Определяем максимальное и минимальное значение температуры и задаем исследуемые интервал [t1;t2].
2. Определяем Z1=f(t1) и Z2=f(t2).
3. Вычисляется
t=t1-(t2-t1)*Z1/(Z2-Z1). (7)
4. Определяются величины P(i) и K(i) по уравнениям (3) и (2).
5. Определяется значение функции Z по уравнению (5), если |t-t2|<ε, то t – корень уравнения.
6. При |t-t2|>ε, если Z*Z2>0, то полагаем t1=t, Z1=Z, иначе полагаем t2=t, Z2=Z. Процесс деления отрезка продолжается, возвращаясь к шагу 2, пока число итераций не превысит заданное значение максимального числа итераций.
Уравнение (7) представляет собой уравнение секущей (хорды) при Z=0.

Рисунок 3. Блок-схема программы для метода половинного деления
program lab1;
uses crt;
label 1,2,3,4,5;
var a,b,c,ti,y,k1,k2,p1,p2,p,ki:array [1..4] of real;
p0,t1,m,t,t2,z1,z2,z,s,s1,s2,e:real;
i,k,n:integer;
begin
clrscr;
writeln('Введите число компонентов');readln(n);
writeln('Введите базовое давление, Р0, ата');readln(p0);
for i:=1 to n do begin
writeln('Компонент ',i);
writeln('Введите коэффициенты уравнения Антуана А,В,С');readln(a[i],b[i],c[i]);
writeln('Введите содержание компонентов смеси Y');readln(y[i]);
end;
writeln('Температуры кипения компонентов смеси');
for i:=1 to n do begin
ti[i]:=b[i]/(a[i]-(ln(p0))/(ln(10)))-c[i];
writeln('T',i,'=',ti[i]:5:2);
end;
writeln('Выберите верхнюю и нижнюю температурную границу');readln(t1,t2);
writeln('Введите погрешность расчета е');readln(e);
for i:=1 to n do begin
p1[i]:=exp((a[i]-b[i]/(c[i]+t1))*ln(10));
p2[i]:=exp((a[i]-b[i]/(c[i]+t2))*ln(10));
k1[i]:=p1[i]/p0;
k2[i]:=p2[i]/p0;
end;
s1:=0; s2:=0;
for i:=1 to n do begin
s1:=s1+y[i]/k1[i];
s2:=s2+y[i]/k2[i];
end;
z1:=s1-1; z2:=s2-1;
if z1*z2<0 then goto 1 else goto 2;
1: k:=0; m:=t2;
3: k:=k+1;
t:=(t1+t2)/2;
for i:=1 to n do begin
p[i]:=exp((a[i]-b[i]/(c[i]+t))*ln(10));
p2[i]:=exp((a[i]-b[i]/(c[i]+t2))*ln(10));
ki[i]:=p[i]/p0;
k2[i]:=p2[i]/p0;
end;
s:=0; s2:=0;
for i:=1 to n do begin
s:=s+y[i]/ki[i];
s2:=s2+y[i]/k2[i];
end;
z:=s-1; z2:=s2-1;
if abs(t-m)<e then goto 4; m:=t;
if z*z2<0 then t1:=t else t2:=t; goto 3;
2: writeln('Неверно выбран интервал'); goto 5;
4: writeln('Температура верха колонны T=',t:5:2);
writeln('Число итераций',k:5);
5: readln;
end.
Результаты расчета по методу половинного деления.
Температуры кипения компонентов
T1=119,14 оС;
Т2=183,78 оС;
Т3=189,71 оС;
Т4=152,89 оС;
T5=183,18 оС.
Точность расчета температуры e=0,1 оС.
Температура верха колонны t=141,137 оС.
Число итераций k=220.
Таблица 1. Зависимость температуры от давления Р0:
| Давление Р0, ата | Метод половинного деления | |||||
| Температура кипения компонентов системы, оС | Температура верха | |||||
| 2,9 | 119,14 | 183,78 | 189,71 | 152,89 | 183,18 | 141,137 |
| 3,0 | 120,55 | 185,39 | 191,34 | 154,42 | 184,80 | 142,647 |
| 3,1 | 121,92 | 186,96 | 192,93 | 155,90 | 186,37 | 144,022 |
| 3,2 | 123,26 | 188,49 | 194,48 | 157,35 | 187,91 | 145,364 |
| 3,3 | 124,57 | 189,99 | 195,99 | 158,77 | 189,41 | 146,674 |
| 3,4 | 125,86 | 191,45 | 197,48 | 160,15 | 190,88 | 147,955 |
| 3,5 | 127,11 | 192,87 | 198,92 | 161,51 | 192,31 | 149,208 |
| 3,6 | 128,33 | 194,27 | 200,34 | 162,83 | 193,71 | 150,434 |
Рисунок 4. График зависимости температуры от давления.
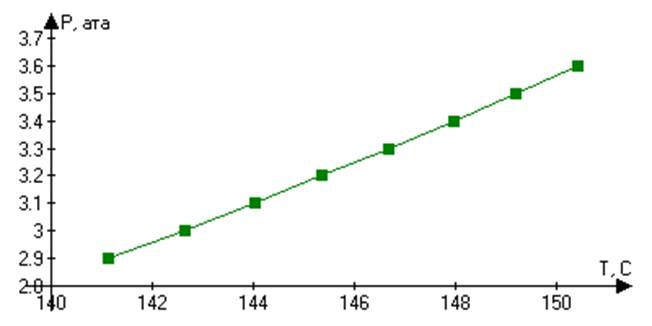
Температура, 0 С
Таблица 2. Идентификаторы параметров программы для расчета по методу половинного деления.
| Параметр | Расшифровка |
| ti pi ki yi р1, р2 k1, k2 А,В,С z t1 t2 t e z1, z2 p0 i n k | Температура кипения i-го компонента, оС Давление насыщенных паров i-го компонента при расчетной температуре, ата Константа фазового равновесия i-го компонента Концентрация i-го компонента в парах, отводимых из колонны, мольные доли Давление насыщенных паров i-го компонента при температуре t1 и t2, ата Константа фазового равновесия i-го компонента при температуре t1 и t2 Коэффициенты уравнения Антуана для i-го компонента Значение итоговой функции при расчетной температуре (уравнение (5)) Нижняя температурная граница интервала температур при расчете температуры верха колонны, оС Верхняя температурная граница интервала температур при расчете температуры верха колонны, оС Расчетная температура, оС Погрешность расчета функции z Значение итоговой функции при температуре t1 и t2 (уравнение (5)) Давление верха колонны, ата Номер компонента Число компонентов Число итераций |
Таблица 3. Проверка независимости конечного результата расчета от исходных граничных температур для расчета по методу половинного деления.
| № | Интервал температур, оС | Число итераций k | Температура верха колонны, оС |
| 0 – 200 | 142,05 | ||
| 100 – 200 | 141,38 | ||
| 140-150 | 141,21 | ||
| 140-145 | 141,20 |
Полученные результаты свидетельствуют о независимости расчета

Рисунок 5. Блок-схема программы для метода хорд (секущих)
program lab2;
uses crt;
label 1,2,3,4,5;
var a,b,c,ti,y,k1,k2,p1,p2,p,ki:array [1..4] of real;
p0,t1,m,t,t2,z1,z2,z,s,s1,s2,e:real;
i,k,n:integer;
begin
clrscr;
writeln('Введите число компонентов');readln(n);
writeln('Введите базовое давление, Р0, ата');readln(p0);
for i:=1 to n do begin
writeln('Компонент ',i);
writeln('Введите коэффициенты уравнения Антуана А,В,С');readln(a[i],b[i],c[i]);
writeln('Введите содержание компонентов смеси Y');readln(y[i]);
end;
writeln('Температуры кипения компонентов смеси');
for i:=1 to n do begin
ti[i]:=b[i]/(a[i]-(ln(p0))/(ln(10)))-c[i];
writeln('T',i,'=',ti[i]:5:2);
end;
writeln('Выберите верхнюю и нижнюю температурную границу');readln(t1,t2);
writeln('Введите погрешность расчета е');readln(e);
for i:=1 to n do begin
p1[i]:=exp((a[i]-b[i]/(c[i]+t1))*ln(10));
p2[i]:=exp((a[i]-b[i]/(c[i]+t2))*ln(10));
k1[i]:=p1[i]/p0;
k2[i]:=p2[i]/p0;
end;
s1:=0; s2:=0;
for i:=1 to n do begin
s1:=s1+y[i]/k1[i];
s2:=s2+y[i]/k2[i];
end;
z1:=s1-1; z2:=s2-1;
if z1*z2<0 then goto 1 else goto 2;
1: k:=0; m:=t2;
3: k:=k+1;
t:=(z1*t2-z2*t1)/(z1-z2);
for i:=1 to n do begin
p[i]:=exp((a[i]-b[i]/(c[i]+t))*ln(10));
p2[i]:=exp((a[i]-b[i]/(c[i]+t2))*ln(10));
ki[i]:=p[i]/p0;
k2[i]:=p2[i]/p0;
end;
s:=0; s2:=0;
for i:=1 to n do begin
s:=s+y[i]/ki[i];
s2:=s2+y[i]/k2[i];
end;
z:=s-1; z2:=s2-1;
if abs(t-m)<e then goto 4; m:=t;
if z*z2<0 then t1:=t else t2:=t; goto 3;
2: writeln('Неверно выбран интервал'); goto 5;
4: writeln('Температура верха колонны T=',t:5:2);
writeln('Число итераций',k:5);
5: readln;
end.






