С ПОМОЩЬЮ ДАТЧИКА ХОЛЛА
Цель работы. Знакомство с принципом действия датчика Холла и использование его для измерения магнитной индукции вдоль оси соленоида.
Введение
Соленоид, представляющий собой пустотелый цилиндр с нанесенной на него обмоткой, широко используется в технике и, в частности, может служить для создания в определенном объеме однородного поля или быть использован для компенсации внешних магнитных полей. Соленоиды применяются, в основном, в тех случаях, когда необходимо создать достаточно интенсивное поле, а размеры устройства, создающего это поле, ограничены,
Получим с помощью закона Био-Савара-Лапласа выражения для индукции магнитного поля на оси кругового тока и оси соленоида. Предположим, что виток круглый и можно пренебречь поперечным сечением провода. Для этих условий вектор индукции магнитного поля в вакууме будет равен
, (1)
где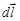 
– элемент проводника с током;
– единичный вектор, направленный от элемента dl к исследуемой точке М;
r – длина отрезка, соединяющего элемент контура dl с точкой М (рис. 1).
Интегрирование ведется по замкнутой линии тока, создающего магнитное поле, В точках, лежащих на оси кругового тока, вектор индукции по условиям симметрии направлен вдоль этой оси, и поэтому достаточно просуммировать проекции на ось векторов индукций от каждого элемента 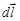. Поскольку элемент 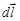составляет с вектором прямой угол, то
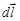|[ , ]| = dl.
 |
Кроме того, как видно из рис. 1,
r2 = R 2 + x 02,
sin q0 = 
,
причем как угол q0, так и расстояние r до точки М одинаковы для всех элементов длины кольца.
Проекция на ось X индукции dB X, создаваемой отдельным элементом длины,
dB X = 
,
поэтому сумма этих проекций будет определяться выражением
(2)
 | |||
 | |||
Выражение (2) позволяет определить индукцию магнитного поля на оси цилиндрической катушки (соленоида) с равномерно распределенными витками. Действительно индукция магнитного поля в точке М (рис. 2), лежащей на оси соленоида, направлена вдоль этой оси и равна сумме индукций магнитного поля, создаваемых в точке М всеми витками. Если w – число витков, приходящееся на единицу длины соленоида, то на малый участок длины dх приходится w dх витков, создающих в точке М поле, индукция которого
dB X = 
w× dх. (3)
Как следует из рис. 2,
r = 
x = R × ctg q,
откуда
dx = - R 
.
С учетом этих соотношений получим
dB X = -m0 
sin q d q.
Приведя интегрирование по всем значениям q, получим
B X = - 
= m0 
(cos q2 - cos q1), (4)
где
cos q1 = - 
, cos q2 = 
.
Пока точка наблюдения находится внутри соленоида и не слишком близко к его краям, магнитное поле остается приблизительно однородным. Нетрудно заметить, что максимальная величина магнитной индукции будет в центре соленоида при х 0 = 0.
Если длина соленоида во много раз больше его радиуса (L >> R), то соленоид можно считать бесконечно длинным. Для точек, расположенных на оси такого соленоида и достаточно удаленных от его концов, q1» p и q2 = 0, и, следовательно, индукция магнитного поля в вакууме будет
B = m0w I. (5)
Так как магнитная проницаемость воздуха приблизительно равна единице (m» 1), можно считать верной эту формулу и для расчета В в воздухе.
Для изучения распределения индукции магнитного поля по длине соленоида в данной работе применяются полупроводниковые элементы, использующие эффект Холла – явление, заключающееся в возникновении э. д. с. при воздействии магнитного поля на ток, протекающий через полупроводник.
Получим выражение для э. д. с. Холла в полупроводнике. Выберем направление вектора 
и тока I X, как указано на рис. 3. Тогда силу Лоренца 
, которая действует на носители тока в полупроводнике n -типа, движущиеся в магнитном поле, можно записать в виде
= - e [ 
, 
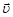], (6)
где 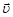– средняя скорость носителей тока в направлении линии тока.
Под влиянием этой силы электроны отклоняются к верхней грани пластины. В результате того, что у нижней грани образуется недостаток электронов, а у верхней избыток: в пластине возникает поперечное электрическое поле с напряженностью 
, направленное для выбранных направлений тока и вектора снизу вверх. Сила е , действующая на электрон, направлена в сторону, противоположную направлению силы Лоренца . В случае равновесного процесса протекания тока по полупроводнику эти силы уравновешиваются, то есть (в проекциях на ось Y)
еЕ = еuB; (7)
 |
E = uB.
Если пластина М достаточно длинная и широкая, то поперечное электрическое поле можно считать однородным. Тогда разность потенциалов U Y между точками А и О равна
U Y = - Ec = - uBc. (8)
Ток в пластине I X обусловлен упорядоченным движением электронов. Если число их в единице объема пластинки равно п 0, а их средняя скорость в направлении линии тока равна u, то силу тока I X можно выразить с помощью формулы
I X = eu п 0 S = eu п 0 ac, (9)
где S = ас –площадь поперечного сечения пластинки.
Заменив в формуле (9) u из соотношения (8), получим
. (10)
Константа R X в выражении (10) называется коэффициентом Холла. Она имеет размерность [м3/A×с]. Как видно, коэффициент Холла определяется концентрацией и знаком носителей тока в полупроводнике.
Из формулы (10) следует, что разность потенциалов, возникающая при прохождении тока через полупроводник, помещенный в магнитное поле, пропорциональна индукции магнитного поля при постоянной силе тока через датчик.
Это явление в настоящее время широко используется для измерения магнитной индукции. Действительно, измерив силу тока в полупроводнике и э. д. с. Холла, можно рассчитать значение магнитной индукции поля, в котором находится полупроводник, по формуле
B = 
. (11)
