В некоторых случаях при проведении регрессионного анализа желательно использовать различные веса наблюдений и вычислить оценки коэффициентов регрессии по методу взвешенных наименьших квадратов. Этот метод обычно применяется, когда дисперсия остатков неоднородна при различных значениях независимых переменных. Можно использовать веса, равные единица на дисперсию остатков и вычислить оценки по методу взвешенных наименьших квадратов. (На практике эти дисперсии обычно не известны, однако они часто пропорциональны значениям независимых переменных, и это пропорциональность может быть использована для вычисления подходящих весов наблюдений.)
40. 
Гетероскедастичность. Метод Голдфельдта-Квандта.
Рассматривая метод наименьших квадратов (см. предыдущие выпуски рассылки), мы обратили внимание на случаи, когда применение МНК ведет кразличным негативным последствиям. Эти случаи заключаются в невыполнении условий применения МНК, одним из которых является независимость остатков и постоянство их дисперсии. Пример, приведенный на рис. 1 показывает, что прогноз значения показателя 
в точке 
значительно отличается от истинного значения. Исходя из критерия минимума среднеквадратической ошибки на точках обучающей последовательности, который является базисом МНК, наилучшим приближением экспериментальной зависимости является прямая. В то же время, очевидно, что дисперсии остатков изменяются по некоторому закону (квадратическому или типа квадратного корня).
В общем случае, такое явление приводит к тому, что оценки параметров по МНК будут несмещенными, состоятельными, но неэффективными и формулу для стандартной ошибки оценки адекватно применять нельзя. Напомним, что:
- оценка 
параметра 
называется несмещенной, если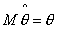 
, где 
- математическое ожидание;
- оценка параметра называется состоятельной, если 
(сходимость по вероятности);
- оценка параметра называется эффективной, если она имеет минимальную дисперсию в некотором классе оценок.
Если дисперсия остатков изменяется для каждого наблюдения или группы наблюдений, т.е. 
, где, в общем случае,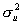 
- неизвестный параметр, а 
- известная симметричная положительно определенная матрица, то такое явление называется гетероскедастичностью. Если же 
, то имеем гомоскедастичность.
В случае простой однофакторной модели 
устранить гетероскедастичность просто. Достаточно левую и правую часть модели поделить на 
. Для многофакторной модели такое преобразование значительно усложняется.
Для проверки наличия гетероскедастичности используют четыре метода, в зависимости от природы исходных данных: критерий 
, параметрический тест Гольдфельда-Квандта, непараметрический тест Гольдфельда-Квандта, тест Глейсера. Приведем алгоритмы каждого из методов.
Параметрический тест Гольдфельда- Квандта применяется, если количество наблюдений невелико и сделано предположение о том, что дисперсия остатков возрастает пропорционально квадрату одной из независимых переменных, т.е. 
.
Шаг 1. Упорядочить наблюдения в соответствии с величиной элементов вектора 
, для которого предположительно выполняется вышеприведенное равенство.
Шаг 2. Исходя из соотношения 
, предложенного авторами метода, где 
- количество элементов , выбросить 
наблюдений, которые находятся в средине вектора.
Шаг 3. Согласно МНК построить две эконометрические модели по двум полученным совокупностям наблюдений размером 
, естественно при условии, что 
, где 
- количество независимых факторов, присутствующих в модели.
Шаг 4. Найти сумму квадратов остатков для первой и второй моделей:
и 
.
Шаг 5. Вычислить значение критерия 
, который соответствует 
- критерию со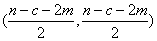 
степенями свободы.
Таким образом, если 
, то гипотеза об отсутствии гетероскедастичности принимается.
