Фиктивные переменные.
В большинстве случаев независимые переменные в регрессионных моделях имеют непрерывные области изменения. Однако теория не накладывает никаких ограничений на характер коэф-тов регрессии, в частности, некоторые переменные могут принимать всего два значения или в более общей ситуации – множество дискретных значений. Необходимость рассмотрения таких переменных возникает в случаях, когда необходимо оценить какой либо качественный признак, т. е. Когда факторы, вводимые в ур-ие регрессии являются кач-ми и не измеряются по числовой шкале. Например, при исследовании зависимости з/п от различных факторов может возникнуть вопрос, влияет ли на ее размер наличие у работника высшего образования; существует ли дискриминация в оплате труда женщин и мужчин. Одним из возможных решений данного примера является оценка отдельных регрессий для каждой категории, а затем изучение различий между ними. Другой подход состоит в оценке единой регрессии с использованием всей совокупности наблюдений и измерений степени влияния качественного фактора посредством введения фиктивной переменной. Она является равноправной переменной наряду с др-ми переменными моделями. Ее фиктивность заключается лишь в том, что она количеств-м образом описывает качественный признак. Второй подход обладает след. преимуществами: 1) это простой способ проверки, является ли воздействие качественного признака значимым; 2) при условии выполнения опред. предположений регрессионной оценки оказывается более эффективным.
Мультиколлинеарность
Слово «коллинеарность» описывает линейную связь между двумя независимыми переменными, тогда как «мультиколлинеарность» – между более чем двумя переменными. На практике всегда используется один термин. Термин «мультиколлинеарность» введен Рагнаром Фришем.
Виды мультиколлинеарности
1. Строгая (perfect) мультиколлинеарность – наличие линейной функциональной связи между независимыми переменными (иногда также и зависимой).
2. Нестрогая (imperfect) мультиколлинеарность – наличие сильной линейной корреляционной связи между независимыми переменными (иногда также и зависимой).
Формула для расчета коэффициентов регрессии в матричном виде.
Представим данные наблюдений и коэффициенты модели в матричной форме.
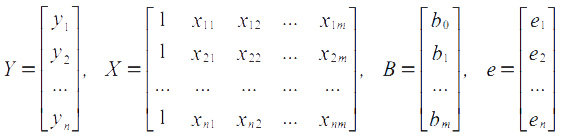
Здесь Y — n-мерный вектор-столбец наблюдений зависимой переменной; X — матрица размерности n х (m +1), в которой i-я строка i = 1, 2,..., n представляет i-е наблюдение вектора значений независимых переменных X1, X2,...,Xm, единица соответствует переменной при свободном члене b0; B — вектор-столбец размерности (m + 1) параметров уравнения множественной регрессии; e — вектор-столбец размерности n отклонений выборочных значений yi зависимой переменной от значений yi, получаемых по уравнению регрессии:
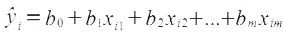
В матричном виде соотношение примет вид:
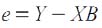
Согласно методу наименьших квадратов:
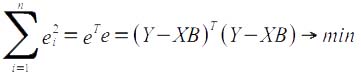
где eT = (e1, e2,..., en), т. е. надстрочный значок T означает транспонированную матрицу.
Можно показать, что предыдущее условие выполняется, если вектор-столбец коэффициентов B найти по формуле:
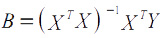
Здесь XT — матрица, транспонированная к матрице X,
(XTX)-1 — матрица, обратная к (XTX). Соотношение справедливо для уравнений регрессии с произвольным количеством m объясняющих переменных






