а) установить, является ли схема симметричной.
Определение. Схема симметрична, если одна ее половина является зеркальным отражением другой. Причем симметрия должна быть не только геометрической, но должны быть симметричны и численные значения сопротивлений или конденсаторов.
Примеры:
1)
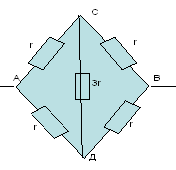
Схема симметричная, так как ветви АСВ и АДВ симметричны геометрически и отношение сопротивления на одном участке АС:АД=1:1 такое же, как и на другом участке СД:ДВ=1:1.
2)
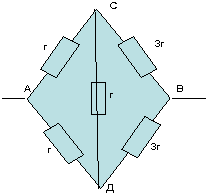
Схема симметричная, так как отношение сопротивлений на участке АС:АД=1:1 такое же, как и на другом участке СВ:ДВ=3:3=1:1
3)

Схема не симметрична, так как отношения сопротивлений численно
не симметричны -1:2 и 1:1.
б) установить точки равных потенциалов.
Пример:

Из соображений симметрии делаем вывод, что в симметричных точках потенциалы равны. В данном случае симметричными точками являются точки С и Д. Таким образом, точки С и Д – эквипотенциальные точки.
в) выбрать, что целесообразно сделать – соединить точки равных потенциалов или же, наоборот, разделить одну точку на несколько точек равных потенциалов.
Мы видим в этом примере, что между точками равных потенциалов С и Д включено сопротивление, по которому ток не будет течь. Следовательно, мы можем отбросить это сопротивление, а точки С и Д соединить в один узел.
г) начертить эквивалентную схему.
Чертим эквивалентную схему. При этом получаем схему с соединенными в одну точку точками С и Д.
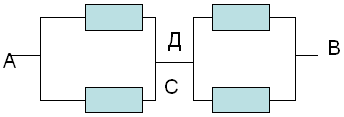
д) найти участки только с последовательным или только с параллельным соединением и рассчитать общее сопротивление на каждом таком участке по законам последовательного и параллельного соединения.
Из полученной эквивалентной схемы видно, что на участке АС мы имеем два параллельно соединенных резистора. Их общее сопротивление находится по закону параллельного соединения:
1/ Rобщ=1/R1+1/R2+1/R3+…
Таким образом 1/RAC=1/r+1/r=2/r,откуда RAC= r/2.
На участке СВ картина аналогичная:
1/RCB= 1/r+1/r =2/r, откуда RCB=r/2.
е)начертить эквивалентную схему, заменяя участки соответствующими им расчетными сопротивлениями.
Чертим эквивалентную схему подставляя в нее рассчитанные сопротивления участков RAC и RCB:
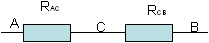
ж)пункты д) и е) повторять до тех пор, пока останется одно сопротивление, величина которого и будет решением задачи.
Повторяем пункт д): на участке АВ имеем два последовательно соединенных сопротивления. Их общее сопротивление находим по закону последовательного соединения:
Rобщ= R1+R2+R3+… то есть, RAB=RAC+RCB = r/2+r/2 =2r/2 = r.
Повторяем пункт е): чертим эквивалентную схему:

Мы получили схему с одним сопротивлением, величина которого равна сопротивлению исходной схемы. Таким образом, мы получили ответ RAB = r.
Далее, для проверки усвоения данного материала можно учащимся предложить задания для самостоятельной работы, взятые из дидактического материала. (см. приложение)






