ПРАКТИЧЕСКАЯ РАБОТА № 21
По дисциплине: МАТЕМАТИКА
Наименование работы: ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ. ОСНОВНЫЕ ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ.
Для специальностей 210705, 210709, 210723.
Составлена преподавателем Калмыковой О. И.
г. Смоленск
2011 г.
Практическая работа № 21.
для студентов 2 курса.
Тема: Основные понятия математической статистики. Основные выборочные характеристики.
1. Цель работы: Изучить основные понятия математической статистики, выборочные характеристики.
2. Литература:
1) Н.В. Богомолов "Практические занятия по математике" М.: Высшая школа, 1990 г.
2) Агапов Г.И., Задачник по теории вероятностей – М.: Высшая школа, 1994.
3) Боровков А. А., Теория вероятностей – М.: Наука, 1986.
4) Вентцель Е.С., Теория вероятностей – М.: Высшая школа, 1999.
3. Подготовка к работе:
1) Изучить теоретический материал по теме: «Основные понятия математической статистики. Основные выборочные характеристики».
2) Подготовить бланк отчета по практической работе.
3) Подготовить ответы на вопросы допуска к работе:
1. Что такое генеральная совокупность?
2. Что такое выборка?
3. Понятие полигона частот.
4. Основное оборудование:
Литература, конспект.
5. Задание:
Выполните задание согласно варианту.
Вариант 1.
1. Определите объем выборки;
2. Представьте выборку в виде вариационного ряда;
3. Определите размах выборки;
4. Представьте выборку статическим рядом;
5. Составьте выборочное распределение;
6. Постройте полигон частот;
7. Определите выборочное среднее и несмещенную выборочную дисперсию.
Числовая выборка:
| Вариант 2.
1. Определите объем выборки;
2. Представьте выборку в виде вариационного ряда;
3. Определите размах выборки;
4. Представьте выборку статическим рядом;
5. Составьте выборочное распределение;
6. Постройте полигон частот;
7. Определите выборочное среднее и несмещенную выборочную дисперсию.
Числовая выборка:
| ||||||||||||||||||||||||||||
| Вариант 3.
1. Определите объем выборки;
2. Представьте выборку в виде вариационного ряда;
3. Определите размах выборки;
4. Представьте выборку статическим рядом;
5. Составьте выборочное распределение;
6. Постройте полигон частот;
7. Определите выборочное среднее и несмещенную выборочную дисперсию.
Числовая выборка:
| Вариант 4. 1. Определите объем выборки; 2. Представьте выборку в виде вариационного ряда; 3. Определите размах выборки; 4. Представьте выборку статическим рядом; 5. Составьте выборочное распределение; 6. Постройте полигон частот; 7. Определите выборочное среднее и несмещенную выборочную дисперсию.
Числовая выборка:
| ||||||||||||||||||||||||||||
| Вариант 5.
1. Определите объем выборки;
2. Представьте выборку в виде вариационного ряда;
3. Определите размах выборки;
4. Представьте выборку статическим рядом;
5. Составьте выборочное распределение;
6. Постройте полигон частот;
7. Определите выборочное среднее и несмещенную выборочную дисперсию.
Числовая выборка:
| Вариант 6.
1. Определите объем выборки;
2. Представьте выборку в виде вариационного ряда;
3. Определите размах выборки;
4. Представьте выборку статическим рядом;
5. Составьте выборочное распределение;
6. Постройте полигон частот;
7. Определите выборочное среднее и несмещенную выборочную дисперсию.
Числовая выборка:
|
6. Порядок выполнения работы:
1.Требование к ТБ;
2. Ответьте на вопросы допуска к работе;
3. Выполните задание, соответствующее варианту.
4. Оформите отчёт;
5. Ответьте на контрольные вопросы.
7. Содержание отчёта:
1. Наименование и цель работы;
2. Результаты выполнения работы;
3. Анализ результатов и выводы.
4. Ответы на контрольные вопросы.
Контрольные вопросы.
1. Что такое генеральная совокупность?
2. Объясните понятие выборка?
3. Чем отличаются друг от друга выборки с повторением и без повторений?
4. Что понимают под представительностью выборки?
5. Дайте понятие вариационного и статистического рядов?
6. Что такое размах выборки?
7. Что называют полигоном частот?
8. Как вычисляется:
1. Выборочное математическое ожидание (выборочное среднее)?
2. Выборочная дисперсия?
9. Дайте понятие точечной оценки.
10. Какая точечная оценка называется смещенной (несмещенной)? Запишите формулы для их нахождения.
Методические указания.
Метод произведений вычисления выборочных средней и дисперсии.
а) Равноотстоящие варианты.
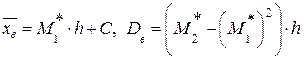 |
Пусть выборка задана в виде распределения равноотстоящих вариант и соответствующих им частот. В этом случае пользуемся формулами:
где h – шаг (разность между двумя соседними вершинами);
С – ложный нуль (варианта, которая расположена примерно в середине вариационного ряда);
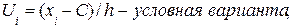 |
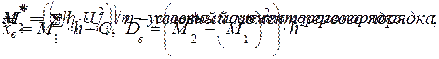 |
б) Неравноотстоящие варианты
1) Интервал делим несколько равных длины h интервалов.
2) Находим середину.
3)
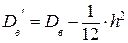 |
В качестве частоты берем сумму частот вариант, попавших в частичный интервал. Так как число интервалов мало, то для вычисления Dв делают поправку Шеппарда:
Метод сумм вычисления выборочных средней и дисперсии.
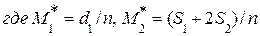
Пусть выборка задана в виде распределения равноотстоящих вариант и соответствующих им частот. В этом случае пользуемся формулами:
d1=a1-в1
S1=a1+в1
S2=a2+в2
Составил преподаватель Калмыкова О.И.






