Область применения: для составления характеристического уравнения, справедливого в отношении любых токов и напряжений исследуемой схемы.
Основные положения: Составить схему свободной составляющей. Полагая сопротивление ёмкости равным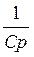 
, а индуктивности – 
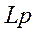, записать систему уравнений для этой схемы либо по законам Кирхгофа, либо по методу контурных токов, либо по методу узловых потенциалов. Главный определитель системы уравнений приравнять нулю. Полученное таким образом уравнение и будет характеристическим.
Пример 4: Составить характеристическое уравнение методом главного определителя для схемы (рис.1).
Решение: Составим схему свободной составляющей. Для получения характеристического уравнения воспользуемся методом контурных токов. Расчетная схема и контурные токи показаны на рис.5.
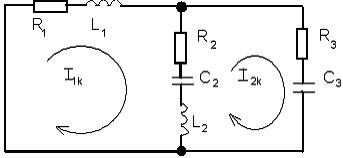
Рис. 5
Контурные уравнения имеют вид:
.
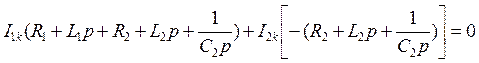
Приравняв главный определитель этой системы уравнений нулю, получим характеристическое уравнение.
.
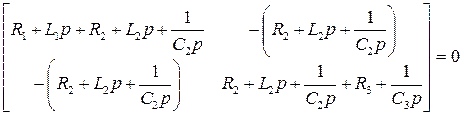После того, как получено характеристическое уравнение, находят корни этого уравнения и записывают выражение свободной составляющей искомого тока. Это выражение зависит от вида корней характеристического уравнения.
а) Все корни имеют кратность равную 1, т.е. среди n корней характеристического уравнения n-й степени нет равных.
,
где 
–неизвестные постоянные интегрирования,
– корни характеристического уравнения. Приведенное выражение для 
справедливо как для действительных корней р, так и для комплексных. Если среди n корней имеются комплексные корни (таких корней всегда четное количество и они попарно комплексно-сопряженные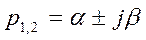 
), то пользоваться таким выражением неудобно.
б) Все корни имеют кратность 1, и среди n корней имеется, например, пара комплексно-сопряженных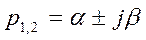
или
.
В последнем выражении A и Ψ являются постоянными интегрирования.
в) Все корни действительны, и среди n корней имеются равные (кратные). Пусть корень p1 имеет кратность, равную m, т.е. p1=p2=….=pm,а остальные – кратность, равную 1, тогда:
.
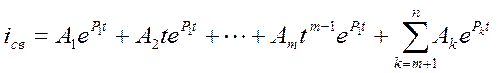Расчет начальных условий
Если схема n-го порядка, то свободная составляющая тока или напряжения содержит n постоянных интегрирований, для определения которых необходимо иметь n начальных условий, соответственно, либо значения тока и его производных до n-1 порядка в момент коммутации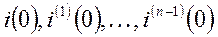 
, либо значения напряжения и его производных до n-1 порядка в момент коммутации 
.
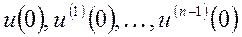Начальные условия условно делят на две группы:
а) независимые начальные условия (ННУ),
б) зависимые начальные условия (ЗНУ).
Независимые начальные условия - значение тока на индуктивности и напряжение на ёмкости в момент коммутации, т.е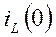 
и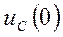 
.
Зависимые начальные условия – значения токов (кроме 
) и их производных любого порядка и напряжений (кроме 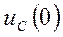) и их производных любого порядка в момент коммутации.
a) Расчет независимых начальных услови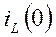й и .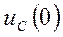
Расчет ННУ проводят на основе анализа режима работы схемы (установившегося или переходного) до коммутации, а именно: рассчитывают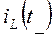 
и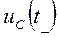 
в соответствующем режиме по схеме до коммутации и в полученные выражения подставляют 
(
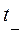в выражениях для и 
означает, что 
и 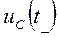– законы изменения соответственно тока на индуктивности и напряжения на емкости до коммутации, 
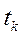– момент коммутации). В результате получаем значения и в момент времени, непосредственно предшествующий коммутации, т.е 
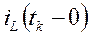и 
.
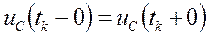
На основании законов коммутаци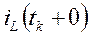и
и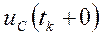 
– значение, соответственно, тока на индуктивности и напряжение на емкости в момент окончания коммутации (длительность коммутации 
).
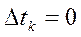Если учесть, что за начало отсчета времени принимают момент коммутации, то искомые НЗУ
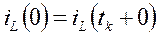
Законы коммутации:
· Ток на индуктивности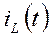 
– непрерывная функция,
· Напряжение на ёмкости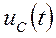 
– непрерывная функция
или
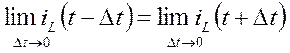
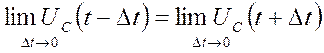
для любого значения t.
б)Расчет зависимых начальных условий
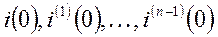либо
.
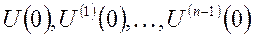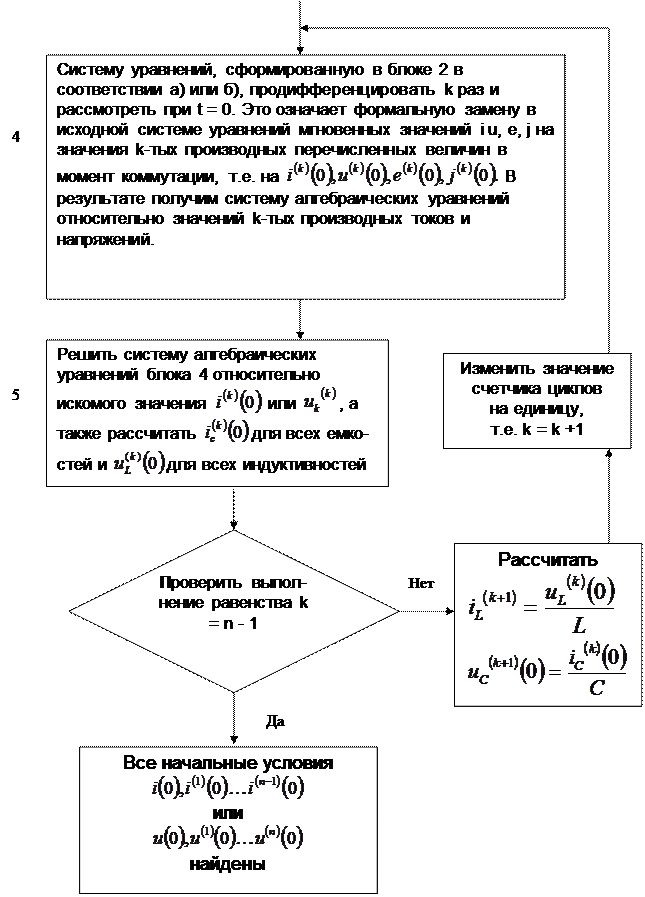
Процедуру расчета ЗНУ представим в виде некоторого циклического алгоритма.
