Правительство Российской Федерации
Федеральное государственное автономное образовательное учреждение
Высшего профессионального образования
«Национальный исследовательский университет
«Высшая школа экономики»
Московский институт электроники и математики
Национального исследовательского университета
«Высшая школа экономики»
Кафедра электроники и наноэлектроники
КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Учебно-методическое пособие
По выполнению расчетно-графической работы
по дисциплине «Теоретические основы электротехники»
Москва 2013
 |
Составитель проф., к.т.н. Е.Г. Осипов
Пособие содержит теоретические положения, необходимые для
выполнения расчетно-графических работ по курсу «Теоретические основы электротехники». Также приведены примеры расчета электрических схем.
УДК 621.3
Классический метод расчета переходных процессов в линейных электрических цепях: Учебно-метод. пособие по выполнению расчетно-графических работ по дисциплине «Теоретические основы электротехники» /
Московский институт электроники и математики Национального
исследовательского университета «Высшая школа экономики»;
Сост. Е.Г. Осипов. М., 2013. 26 с.
Ил. 16, библиогр. 4 назв.
ISBN 978-5-94506-311-2
 |
Классический метод расчета переходных процессов в линейных
Электрических цепях
Суть классического метода расчета переходных процессов в линейных электрических цепях заключается в непосредственном решении системы линейных дифференциальных уравнений.
Любую схему замещения после коммутации можно однозначно описать с помощью системы независимых уравнений, составленных по законам Кирхгофа (ЗК).
Если эту систему уравнений решить относительно тока какой- либо ветви с учетом уравнений связи между током и напряжением на пассивных элементах, соответственно на сопротивлении, емкости и индуктивности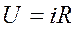 
, 
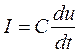и 
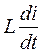, то получаем линейное неоднородное дифференциальное уравнение n-го порядка вида:
или 
или 
где 
.
Решение такого уравнения предоставляют в виде суммы двух слагаемых:
,
где 
- свободная составляющая тока;
- принужденная составляющая тока;
- общее решение однородного дифференциального уравнения.
,
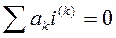форма записи которого зависит от вида корней характеристического уравнения. Характеристическое уравнение получают заменой в однородном дифференциальном уравнении k-той производной тока на переменную p в k-той степени, т.е. 
заменяют на 
.
Характеристическое уравнение имеет вид:
- частное решение неоднородного дифференциального уравнения, которое рассчитывают по виду правой части указанного уравнения.
Процедуру расчета переходных процессов можно разделить на 4 основных этапа:
1. Расчет принужденной составляющей тока 
.
2. Составление характеристического уравнения и определение его корней.
3. Расчет начальных условий.
4. Определение постоянных интегрирования.
Рассмотрим подробно каждый этап.
Расчет принужденной составляющей
Расчет принужденной составляющей зависит от вида источников эдс e и источников тока j в исследуемой схеме. Если источники постоянные, или гармонические одной и той же частоты, или периодические негармонические, то принужденную составляющую определяют, рассчитывая соответствующий установившийся режим в схеме после коммутации.
а) Источники постоянные: 
, 
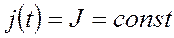
определяют на основе анализа схемы установившегося режима постоянного тока (УРПТ) после коммутации. Для получения схемы УРПТ после коммутации необходимо в исходной схеме после коммутации сделать следующие замены:
Правомочность такой замены вытекает из того, что в установившемся режиме постоянного тока, по определению, токи и напряжения на всех элементах постоянны.
Для тока и напряжения на емкости и индуктивности справедливы соответственно уравнения
и 
.
В УРПТ, согласно определению, 
и 
и, следовательно, 
и 
. Эти равенства означают, что на схеме замещения ветви с емкостями можно разомкнуть, и зажимы, между которыми включены индуктивности, закоротить.
В результате таких преобразований получаем резистивную эквивалентную схему, по которой проводят расчет 
любым рациональным методом из рассмотренных в разделе «Анализ резистивных схем».
a) Источники гармонические одной и той же частоты
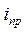определяют на основе анализа установившегося режима гармонического тока (УРГТ) в схеме после коммутации. Расчет УРГТ проводят комплексным методом. Для этого по исходной схеме после коммутации составляют комплексную схему замещения и рассчитывают комплексное действующее значение искомого тока 
, а затем переходят к мгновенному значению
б) Источники периодические негармонические.
определяют на основе расчета установившегося режима периодического негармонического тока. Для этого периодические негармонические функции источников предоставляют в виде конечных тригонометрических рядов Фурье
,
где k – номер гармоники и принимает значение от 1 до n.
Затем, применяя принцип наложения, рассчитывают составляющие принужденной составляющей на каждой гармонике:
- на нулевой гармонике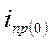 
(постоянные источники 
) в соответствии с пунктом а
- на каждой k-той гармонике 
(гармонические источники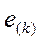 
) в соответствии с пунктом б.
Искомая принужденная составляющая тока
.
Если в схеме источники непериодические, то для расчета принужденной составляющей необходимо по схеме после коммутации на основе законов Кирхгофа получить неоднородное дифференциальное уравнение. Записать выражение для 
аналогичные виду правой части уравнения с неизвестными коэффициентами и подставить в дифференциальное уравнение. Затем приравнять коэффициенты у подобных членов справа и слева. В результате получают систему уравнений для расчета неизвестных коэффициентов. Следует заметить, что если источники непериодические, то расчет принужденной составляющей часто требует больших трудозатрат. Поэтому в этих случаях, как правило, анализ переходных процессов проводят операторным, а не классическим методом.
